
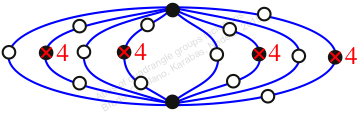
Reflexible,
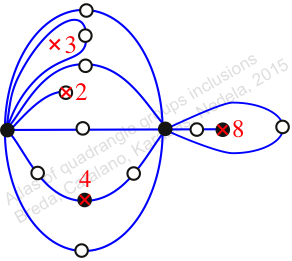
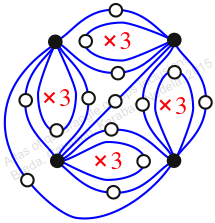
Case: 4
πz = (1, 2)
πw = id
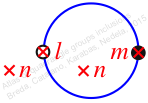
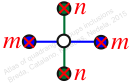
Reflexible,
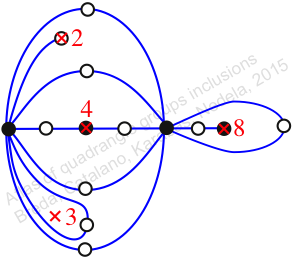
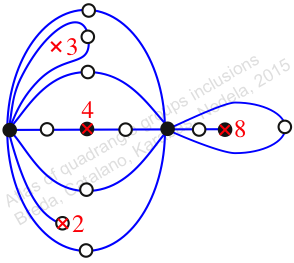
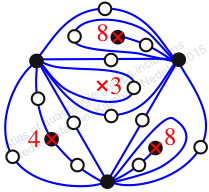
Case: 4
πz = (1, 2)
πw = id
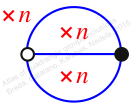
Reflexible,
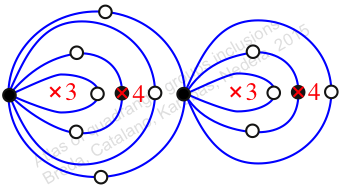
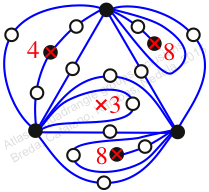
Case: 3
πy = (1, 2)
πz = id
πw = id

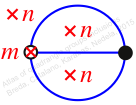
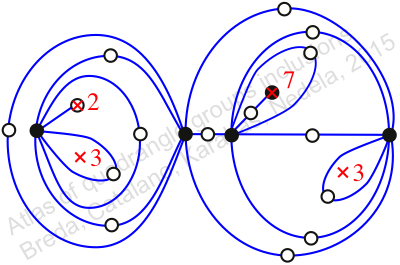
Reflexible,
Case: 4
πz = (1, 2, 3)
πw = (2, 3)

Reflexible,
Case: 4
πz = (1, 2, 3)
πw = (2, 3)
Reflexible,
Case: 2
πz = (1, 3, 2)
πw = id

Reflexible,
Case: 3
πz = (1, 2)
πw = (2, 3)
Reflexible,
Case: 2
πz = (1, 3, 2)
πw = id

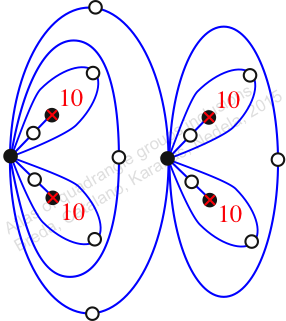
Reflexible,
Case: 4
πz = (2, 3, 4)
πw = (1, 2, 4, 3)
Reflexible,
Case: 4
πz = (2, 3, 4)
πw = (1, 2, 3)

Reflexible,
Case: 3
πz = (1, 2, 4, 3)
πw = (1, 2)(3, 4)

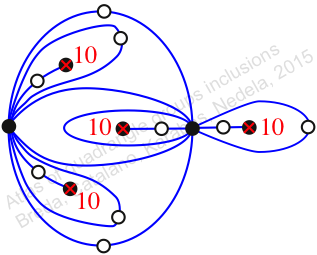
Reflexible,
Case: 2
πz = (1, 2, 4, 3)
πw = (2, 3)

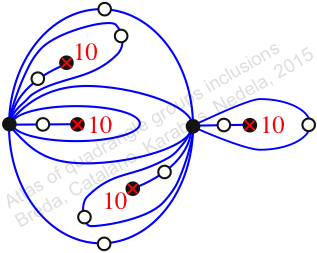
Reflexible,
Case: 3
πz = (1, 2, 4, 3)
πw = (2, 3, 4)

Reflexible,
Case: 3
πz = (1, 2)(3, 4)
πw = (1, 3)(2, 4)
Reflexible,
Case: 3
πz = (2, 3, 4)
πw = (1, 2, 3)

Reflexible,
Case: 2
πz = (1, 2, 4, 3)
πw = (2, 3)

Reflexible,
Case: 4
πz = (1, 2, 3)
πw = (1, 2)(3, 4)

Reflexible,
Case: 4
πz = (1, 3, 4)
πw = (1, 2, 3)
Reflexible,
Case: 2
πz = (1, 2, 4, 3)
πw = (3, 4)

Reflexible,
Case: 1
πz = (1, 3, 4, 2)
πw = id
Reflexible,
Case: 1
πy = (1, 3)(2, 4)
πz = (1, 4)(2, 3)
πw = id
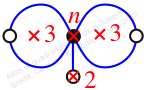
Reflexible,
Case: 4
πz = (2, 3, 4)
πw = (1, 2, 4, 5, 3)
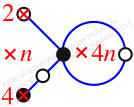
Chiral,
Mirror of 24,
Case: 4
πz = (2, 3, 5, 4)
πw = (1, 2, 4, 3)
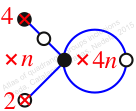
Chiral,
Mirror of 23,
Case: 4
πz = (2, 3, 4, 5)
πw = (1, 2, 4, 3)
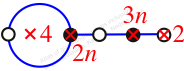
Reflexible,
Case: 4
πz = (2, 3, 5, 4)
πw = (1, 2, 3)(4, 5)

Reflexible,
Case: 2
πz = (1, 2, 4, 5, 3)
πw = (2, 3)(4, 5)
Reflexible,
Case: 2
πz = (1, 2, 4, 5, 3)
πw = (2, 3, 4)

Reflexible,
Case: 2
πz = (2, 3, 5, 4)
πw = (1, 2, 4, 5, 3)
Reflexible,
Case: 3
πz = (1, 3, 2)
πw = (1, 2, 4, 5, 3)
Reflexible,
Case: 4
πz = (2, 4, 3, 5)
πw = (1, 2, 5, 3)
Reflexible,
Case: 2
πz = (2, 3, 5)
πw = (1, 2, 4, 5, 6, 3)
Reflexible,
Case: 2
πz = (1, 2, 4)(3, 6, 5)
πw = (1, 3)(2, 5)(4, 6)
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)
πw = (1, 3, 4)(2, 5, 6)
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)
πw = (1, 3, 6, 4)(2, 5)
Reflexible,
Case: 2
πz = (1, 2, 3)(4, 6, 5)
πw = (2, 3, 5, 4)
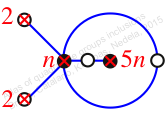
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)
πw = (2, 3, 5, 6, 4)
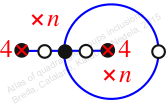
Reflexible,
Case: 3
πz = (2, 3, 5, 4)
πw = (1, 2, 3)(4, 6, 5)
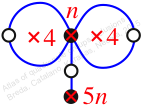
Reflexible,
Case: 3
πz = (2, 3, 4, 5)
πw = (1, 2, 4, 6, 3)
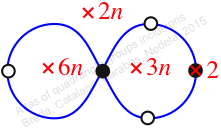
Reflexible,
Case: 2
πz = (1, 2, 4, 3)(5, 6)
πw = (2, 3, 5)(4, 6)
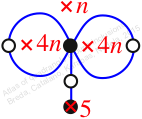
Reflexible,
Case: 2
πz = (2, 3, 6, 4, 5)
πw = (1, 2, 4, 3)
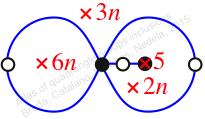
Reflexible,
Case: 2
πz = (2, 3, 5, 6, 4)
πw = (1, 2, 3)(4, 5)
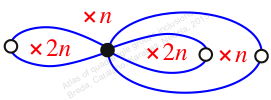
Reflexible,
Case: 1
πz = (1, 2, 4, 6, 5, 3)
πw = (2, 3)(4, 5)
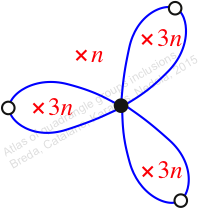
Reflexible,
Case: 1
πz = (1, 2, 4, 5, 6, 3)
πw = (2, 3, 5)
Reflexible,
Case: 1
πz = (1, 5, 2)(3, 4, 6)
πw = (2, 4)(3, 5)
Chiral,
Mirror of 46,
Case: 4
πz = (1, 2, 4, 3)(5, 6)
πw = (2, 3, 5, 6, 4)
Chiral,
Mirror of 45,
Case: 4
πz = (1, 2, 4, 3)(5, 6)
πw = (2, 3, 4, 6, 5)
Reflexible,
Case: 4
πz = (2, 3, 4, 5)
πw = (1, 2, 4, 6, 3)
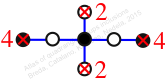
Chiral,
Mirror of 49,
Case: 3
πz = (2, 3, 5, 4)
πw = (1, 2, 4, 6, 5, 3)
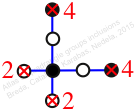
Chiral,
Mirror of 48,
Case: 3
πz = (2, 3, 5, 4)
πw = (1, 2, 4, 5, 6, 3)
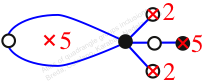
Reflexible,
Case: 4
πz = (2, 3, 5, 6, 4)
πw = (1, 2, 4, 5, 3)

Chiral,
Mirror of 52,
Case: 4
πz = (2, 3, 5, 6, 4)
πw = (1, 2, 4, 6, 3)
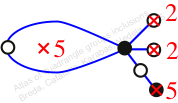
Chiral,
Mirror of 51,
Case: 4
πz = (2, 3, 6, 4, 5)
πw = (1, 2, 4, 6, 3)
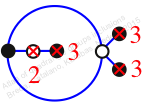
Reflexible,
Case: 2
πz = (1, 2, 3)(4, 5, 6)
πw = (1, 2)(3, 4, 6, 5)
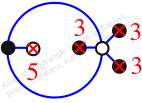
Reflexible,
Case: 2
πz = (1, 3, 2)(4, 5, 6)
πw = (1, 2, 4, 6, 3)
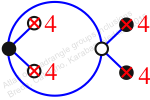
Reflexible,
Case: 3
πz = (3, 5, 6, 4)
πw = (1, 2, 4, 3)
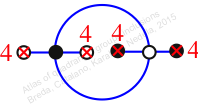
Reflexible,
Case: 3
πz = (2, 4, 3, 6)
πw = (1, 2, 5, 3)
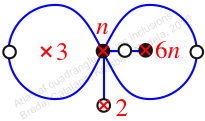
Chiral,
Mirror of 58,
Case: 4
πz = (2, 3, 4)(5, 7, 6)
πw = (1, 2, 4, 6, 5, 3)
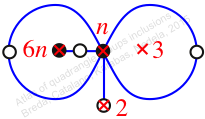
Chiral,
Mirror of 57,
Case: 4
πz = (2, 3, 5)(4, 6, 7)
πw = (1, 2, 4, 6, 5, 3)
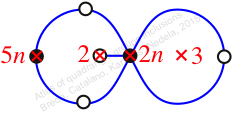
Reflexible,
Case: 4
πz = (2, 3, 5)(4, 7, 6)
πw = (1, 2, 4, 6, 3)(5, 7)
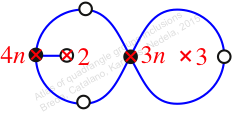
Reflexible,
Case: 4
πz = (2, 3, 5)(4, 6, 7)
πw = (1, 2, 4, 3)(5, 7, 6)
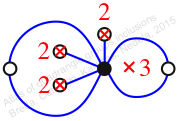
Chiral,
Mirror of 62,
Case: 2
πz = (2, 3, 4)(5, 7, 6)
πw = (1, 2, 4, 6, 7, 5, 3)
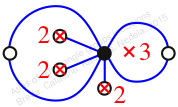
Chiral,
Mirror of 61,
Case: 2
πz = (2, 3, 5)(4, 6, 7)
πw = (1, 2, 4, 7, 6, 5, 3)
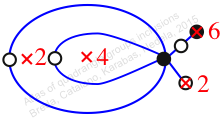
Chiral,
Mirror of 64,
Case: 4
πz = (2, 3)(4, 5, 7, 6)
πw = (1, 2, 4, 6, 5, 3)
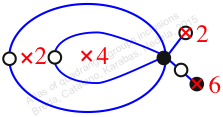
Chiral,
Mirror of 63,
Case: 4
πz = (2, 3)(4, 5, 6, 7)
πw = (1, 2, 4, 6, 5, 3)
Chiral,
Mirror of 66,
Case: 4
πz = (2, 3, 4, 5)(6, 7)
πw = (1, 2, 4, 7, 6, 3)

Chiral,
Mirror of 65,
Case: 4
πz = (2, 3, 6, 5)(4, 7)
πw = (1, 2, 4, 7, 5, 3)
Reflexible,
Case: 2
πz = (2, 3, 5, 4)
πw = (1, 2, 4, 7, 5, 6, 3)
Chiral,
Mirror of 70,
Case: 4
πz = (2, 3, 5, 7, 4)
πw = (1, 2, 4, 5, 6, 3)
Reflexible,
Case: 4
πz = (2, 3, 5, 6, 4)
πw = (1, 2, 4, 7, 6, 3)
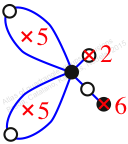
Chiral,
Mirror of 68,
Case: 4
πz = (2, 3, 6, 7, 5)
πw = (1, 2, 4, 5, 6, 3)

Reflexible,
Case: 4
πz = (1, 2, 3)(4, 5, 7)
πw = (1, 2)(3, 4, 6, 5)
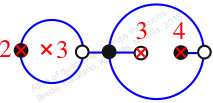
Reflexible,
Case: 4
πz = (1, 3, 4)(2, 5, 6)
πw = (1, 2, 5, 3)(6, 7)
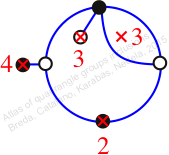
Chiral,
Mirror of 74,
Case: 4
πz = (1, 3, 4)(5, 7, 6)
πw = (1, 2, 5, 3)(4, 7)
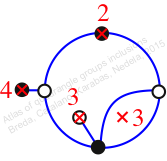
Chiral,
Mirror of 73,
Case: 4
πz = (1, 3, 4)(2, 6, 7)
πw = (1, 2, 5, 3)(4, 7)

Reflexible,
Case: 4
πz = (1, 3, 4)(2, 6, 7)
πw = (1, 2, 5, 6, 3)
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 6, 7)
πw = (1, 2, 4, 3)(5, 7, 8, 6)

Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 6)
πw = (1, 2, 4, 8, 6, 3)(5, 7)
Reflexible,
Case: 3
πz = (2, 3, 5)(6, 8, 7)
πw = (1, 2, 4, 5, 7, 6, 3)
Reflexible,
Case: 1
πz = (1, 2, 5, 4)(3, 7, 8, 6)
πw = (1, 3)(2, 6)(4, 7)(5, 8)
Reflexible,
Case: 1
πz = (1, 2, 4, 3)(5, 7, 8, 6)
πw = (2, 3, 5)(4, 6, 7)
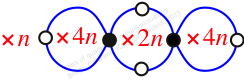
Reflexible,
Case: 1
πz = (1, 2, 4, 3)(5, 8, 6, 7)
πw = (2, 3, 6, 5)(4, 7)
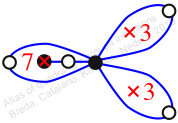
Reflexible,
Case: 2
πz = (2, 3, 5)(6, 8, 7)
πw = (1, 2, 4, 5, 7, 6, 3)
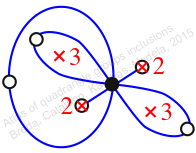
Chiral,
Mirror of 85,
Case: 3
πz = (2, 3, 4)(5, 7, 6)
πw = (1, 2, 4, 6, 8, 7, 5, 3)
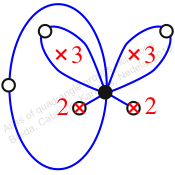
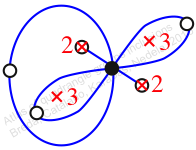
Reflexible,
Case: 3
πz = (2, 3, 4)(5, 7, 6)
πw = (1, 2, 4, 6, 7, 8, 5, 3)
Chiral,
Mirror of 83,
Case: 3
πz = (2, 3, 5)(4, 6, 7)
πw = (1, 2, 4, 7, 8, 6, 5, 3)
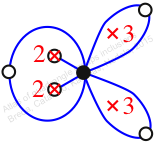
Reflexible,
Case: 3
πz = (2, 3, 5)(6, 8, 7)
πw = (1, 2, 4, 5, 7, 8, 6, 3)
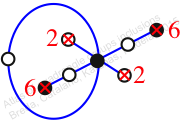
Chiral,
Mirror of 89,
Case: 3
πz = (1, 2, 4, 3)(5, 6, 8, 7)
πw = (2, 3, 5, 7, 6, 4)
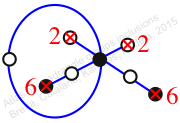
Reflexible,
Case: 3
πz = (1, 2, 4, 3)(5, 6, 7, 8)
πw = (2, 3, 5, 7, 6, 4)
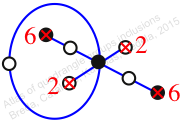
Chiral,
Mirror of 87,
Case: 3
πz = (1, 2, 4, 3)(5, 7, 8, 6)
πw = (2, 3, 4, 6, 7, 5)
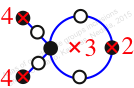
Reflexible,
Case: 2
πz = (2, 3, 6, 5)(7, 8)
πw = (1, 2, 4, 5, 7, 3)(6, 8)
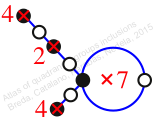
Chiral,
Mirror of 92,
Case: 2
πz = (2, 3)(4, 5, 6, 7)
πw = (1, 2, 4, 6, 8, 5, 3)
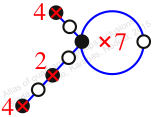
Chiral,
Mirror of 91,
Case: 2
πz = (2, 3)(4, 5, 8, 7)
πw = (1, 2, 4, 6, 7, 5, 3)
Reflexible,
Case: 1
πz = (2, 3, 6, 5)
πw = (1, 2, 4, 5, 8, 6, 7, 3)
Reflexible,
Case: 2
πz = (2, 3, 6, 8, 5)
πw = (1, 2, 4, 5, 6, 7, 3)
Reflexible,
Case: 3
πz = (2, 3, 6, 7, 8, 5)
πw = (1, 2, 4, 5, 7, 3)
Reflexible,
Case: 3
πz = (2, 3, 6, 7, 4, 5)
πw = (1, 2, 4, 8, 7, 3)
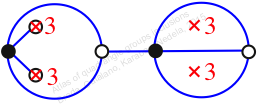
Reflexible,
Case: 3
πz = (1, 3, 2)(4, 7, 5)
πw = (1, 2, 4, 3)(5, 6, 8, 7)
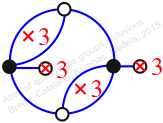
Reflexible,
Case: 3
πz = (1, 3, 4)(5, 8, 6)
πw = (1, 2, 5, 3)(4, 7, 6, 8)
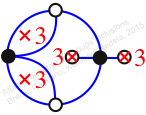
Reflexible,
Case: 3
πz = (1, 3, 4)(2, 7, 5)
πw = (1, 2, 5, 3)(4, 8, 7, 6)
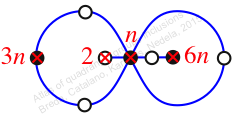
Reflexible,
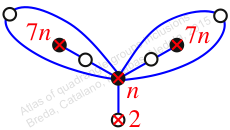
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 8, 9)
πw = (2, 3, 5, 8, 7, 4)(6, 9)
Reflexible,
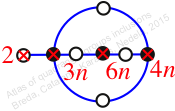
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 8, 9)
πw = (2, 3, 5, 7, 8, 6, 4)
Reflexible,
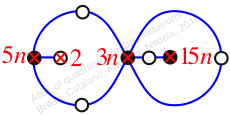
Case: 2
πz = (1, 2, 3)(4, 8, 5)(6, 9, 7)
πw = (1, 3, 7, 4)(2, 5, 6)(8, 9)
Reflexible,
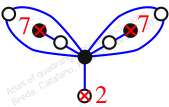
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 9, 8)
πw = (2, 3, 5, 7, 4)(6, 8, 9)
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 8, 9)
πw = (2, 3, 5, 7, 8, 6, 4)
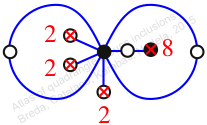
Chiral,
Mirror of 106,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 8, 9)
πw = (2, 3, 5, 7, 9, 8, 6, 4)
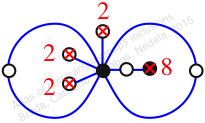
Chiral,
Mirror of 105,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 9, 8)
πw = (2, 3, 5, 6, 8, 9, 7, 4)
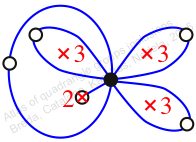
Chiral,
Mirror of 108,
Case: 2
πz = (2, 3, 4)(5, 7, 6)
πw = (1, 2, 4, 6, 9, 7, 8, 5, 3)
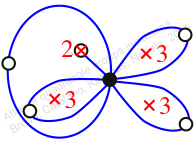
Chiral,
Mirror of 107,
Case: 2
πz = (2, 3, 5)(4, 6, 8)
πw = (1, 2, 4, 7, 8, 9, 6, 5, 3)
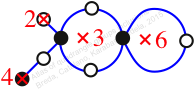
Chiral,
Mirror of 112,
Case: 4
πz = (2, 3, 5, 4)(6, 9, 7, 8)
πw = (1, 2, 4, 7, 6, 3)(5, 8)
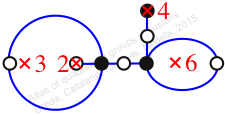
Chiral,
Mirror of 111,
Case: 4
πz = (2, 3, 4, 5)(6, 8, 9, 7)
πw = (1, 2, 4, 7, 6, 3)(8, 9)
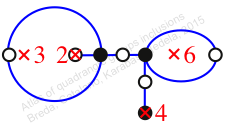
Chiral,
Mirror of 110,
Case: 4
πz = (2, 3, 6, 5)(4, 7, 9, 8)
πw = (1, 2, 4, 7, 5, 3)(8, 9)
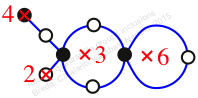
Chiral,
Mirror of 109,
Case: 4
πz = (2, 3, 6, 5)(4, 7, 8, 9)
πw = (1, 2, 4, 8, 6, 3)(5, 7)
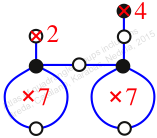
Chiral,
Mirror of 115,
Case: 4
πz = (2, 3, 4, 5)(6, 8, 9, 7)
πw = (1, 2, 4, 7, 8, 6, 3)
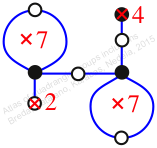
Chiral,
Mirror of 116,
Case: 4
πz = (2, 3, 4, 5)(6, 8, 9, 7)
πw = (1, 2, 4, 7, 9, 6, 3)
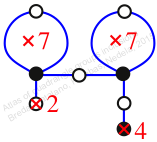
Chiral,
Mirror of 115,
Case: 4
πz = (2, 3, 6, 5)(4, 7, 9, 8)
πw = (1, 2, 4, 8, 7, 5, 3)
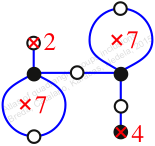
Chiral,
Mirror of 114,
Case: 4
πz = (2, 3, 6, 5)(4, 7, 8, 9)
πw = (1, 2, 4, 8, 7, 5, 3)
Reflexible,
Case: 2
πz = (1, 3, 2)(4, 7, 5)(6, 9, 8)
πw = (1, 2, 4, 3)(5, 6, 8, 7)
Reflexible,
Case: 2
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)
πw = (1, 2, 4, 7, 5, 9, 6, 3)
Reflexible,
Case: 2
πz = (2, 3, 5)(4, 7, 6)(8, 9, 10)
πw = (1, 2, 4, 8, 9, 6, 3)(5, 7)
Reflexible,
Case: 2
πz = (2, 3, 5)(4, 6, 7)(8, 10, 9)
πw = (1, 2, 4, 3)(5, 7, 9, 8, 6)
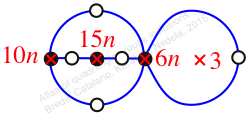
Reflexible,
Case: 2
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)
πw = (1, 2, 4, 6, 3)(5, 9, 7)(8, 10)
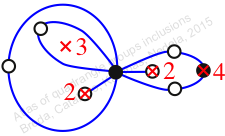
Chiral,
Mirror of 123,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 9, 10)
πw = (1, 2, 4, 6, 9, 8, 5, 3)(7, 10)
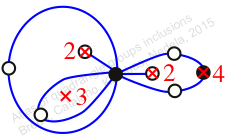
Chiral,
Mirror of 122,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 10, 9)
πw = (1, 2, 4, 7, 9, 6, 5, 3)(8, 10)
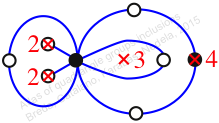
Reflexible,
Case: 4
πz = (2, 3, 5)(4, 7, 6)(8, 9, 10)
πw = (1, 2, 4, 8, 10, 9, 6, 3)(5, 7)
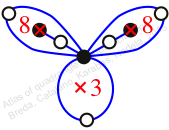
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)
πw = (1, 2, 4, 7, 5, 9, 6, 3)
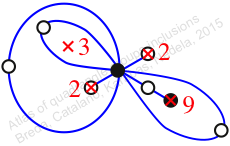
Chiral,
Mirror of 128,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 9, 10)
πw = (1, 2, 4, 6, 8, 9, 7, 5, 3)
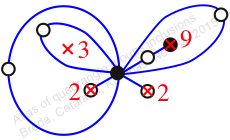
Chiral,
Mirror of 129,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 10, 9)
πw = (1, 2, 4, 6, 7, 9, 8, 5, 3)
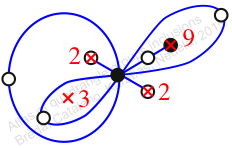
Chiral,
Mirror of 126,
Case: 4
πz = (2, 3, 5)(4, 6, 7)(8, 10, 9)
πw = (1, 2, 4, 7, 9, 8, 6, 5, 3)
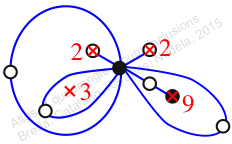
Chiral,
Mirror of 127,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 9, 10)
πw = (1, 2, 4, 7, 9, 8, 6, 5, 3)
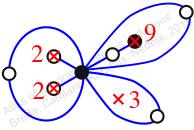
Chiral,
Mirror of 131,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)
πw = (1, 2, 4, 7, 5, 9, 10, 6, 3)
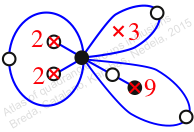
Chiral,
Mirror of 130,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)
πw = (1, 2, 4, 8, 7, 5, 9, 6, 3)
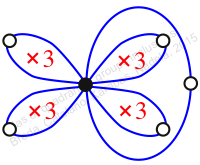
Reflexible,
Case: 1
πz = (2, 3, 5)(6, 8, 7)
πw = (1, 2, 4, 5, 7, 10, 8, 9, 6, 3)
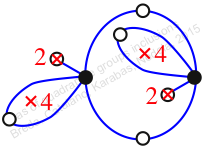
Reflexible,
Case: 3
πz = (2, 3, 5, 4)(6, 8, 9, 7)
πw = (1, 2, 4, 6, 3)(5, 7, 9, 10, 8)
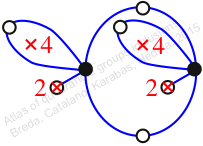
Chiral,
Mirror of 135,
Case: 3
πz = (2, 3, 5, 4)(6, 8, 10, 7)
πw = (1, 2, 4, 6, 3)(5, 7, 9, 10, 8)
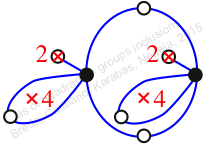
Chiral,
Mirror of 134,
Case: 3
πz = (2, 3, 6, 5)(4, 7, 9, 8)
πw = (1, 2, 4, 6, 3)(5, 8, 9, 10, 7)
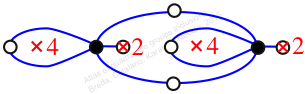
Reflexible,
Case: 3
πz = (2, 3, 6, 5)(4, 8, 9, 7)
πw = (1, 2, 4, 7, 3)(5, 6, 9, 10, 8)
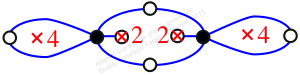
Reflexible,
Case: 3
πz = (2, 3, 6, 5)(4, 8, 10, 7)
πw = (1, 2, 4, 7, 3)(5, 9, 6, 10, 8)
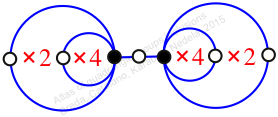
Reflexible,
Case: 1
πz = (2, 3)(4, 5, 7, 6)(8, 9)
πw = (1, 2, 4, 5, 3)(6, 8, 10, 9, 7)
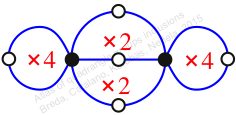
Reflexible,
Case: 1
πz = (2, 3, 6, 5)(4, 8)(7, 10)
πw = (1, 2, 4, 7, 3)(5, 9, 6, 10, 8)
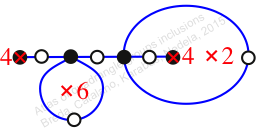
Chiral,
Mirror of 141,
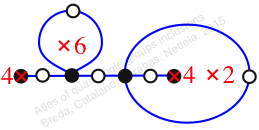
Case: 3
πz = (2, 3, 5, 4)(6, 7, 8, 9)
πw = (1, 2, 3)(4, 6, 8, 10, 7, 5)
Chiral,
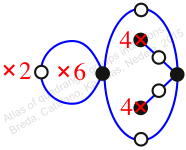
Mirror of 140,
Case: 3
πz = (2, 3, 5, 4)(6, 7, 10, 9)
πw = (1, 2, 3)(4, 6, 8, 9, 7, 5)
Reflexible,
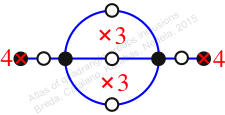
Case: 3
πz = (2, 3, 6, 5)(7, 9, 10, 8)
πw = (1, 2, 4, 5, 7, 3)(6, 8, 9)
Reflexible,
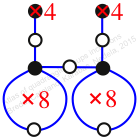
Case: 3
πz = (2, 3, 6, 5)(4, 8, 10, 7)
πw = (1, 2, 4, 9, 7, 3)(5, 8)(6, 10)
Reflexible,
Case: 3
πz = (2, 3, 4, 5)(6, 8, 10, 7)
πw = (1, 2, 4, 7, 8, 9, 6, 3)
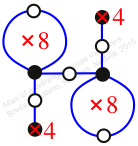
Chiral,
Mirror of 146,
Case: 3
πz = (2, 3, 4, 5)(6, 8, 9, 7)
πw = (1, 2, 4, 7, 10, 9, 6, 3)
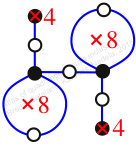
Chiral,
Mirror of 145,
Case: 3
πz = (2, 3, 6, 5)(4, 7, 8, 9)
πw = (1, 2, 4, 8, 10, 7, 5, 3)
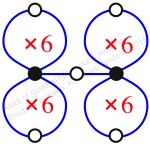
Reflexible,
Case: 1
πz = (1, 2, 4, 6, 3)(5, 8, 9, 10, 7)
πw = (2, 3, 4, 7, 9, 5)
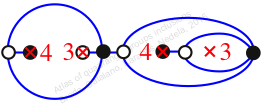
Reflexible,
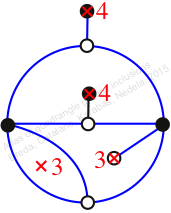
Case: 4
πz = (1, 3, 4)(2, 5, 6)(7, 8, 10)
πw = (1, 2, 5, 3)(6, 7, 9, 8)
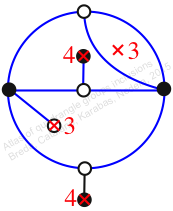
Chiral,
Mirror of 151,
Case: 4
πz = (1, 3, 4)(2, 10, 9)(5, 8, 7)
πw = (1, 2, 5, 3)(4, 8, 10, 6)
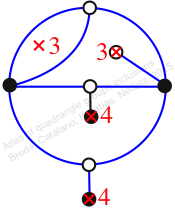
Reflexible,
Case: 4
πz = (1, 3, 4)(2, 6, 9)(5, 8, 7)
πw = (1, 2, 5, 3)(4, 8, 10, 9)
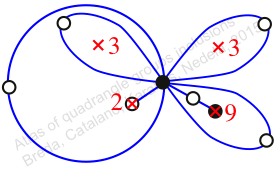
Chiral,
Mirror of 149,
Case: 4
πz = (1, 3, 4)(2, 6, 9)(5, 10, 7)
πw = (1, 2, 5, 3)(4, 8, 7, 9)
Chiral,
Mirror of 154,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(9, 10, 11)
πw = (1, 2, 4, 6, 9, 10, 7, 8, 5, 3)
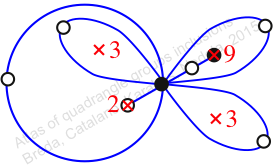
Chiral,
Mirror of 155,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 11, 10)
πw = (1, 2, 4, 6, 9, 7, 10, 8, 5, 3)
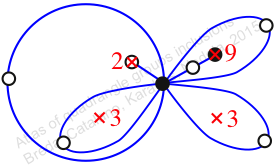
Chiral,
Mirror of 152,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(9, 11, 10)
πw = (1, 2, 4, 7, 8, 10, 9, 6, 5, 3)
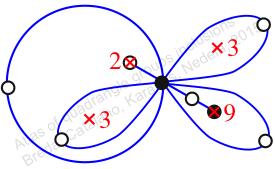
Chiral,
Mirror of 153,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 10, 11)
πw = (1, 2, 4, 7, 10, 8, 9, 6, 5, 3)
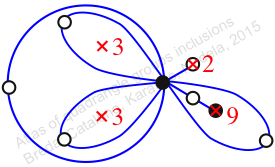
Chiral,
Mirror of 157,
Case: 4
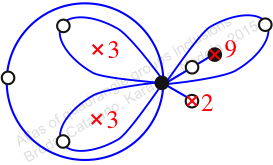
πz = (2, 3, 5)(6, 8, 7)(9, 10, 11)
πw = (1, 2, 4, 5, 7, 9, 10, 8, 6, 3)
Chiral,
Mirror of 156,
Case: 4
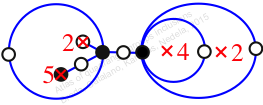
πz = (2, 3, 5)(6, 8, 7)(9, 11, 10)
πw = (1, 2, 4, 5, 7, 8, 10, 9, 6, 3)
Chiral,
Mirror of 159,
Case: 4
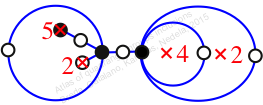
πz = (2, 3)(4, 5, 7, 6)(8, 9, 11, 10)
πw = (1, 2, 4, 5, 3)(6, 8, 10, 9, 7)
Chiral,
Mirror of 158,
Case: 4
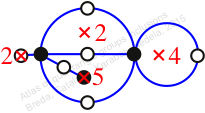
πz = (2, 3)(4, 5, 7, 6)(8, 9, 10, 11)
πw = (1, 2, 4, 5, 3)(6, 8, 10, 9, 7)
Chiral,
Mirror of 161,
Case: 4
πz = (2, 3, 6, 5)(4, 8)(7, 10, 11, 9)
πw = (1, 2, 4, 7, 3)(5, 6, 9, 10, 8)
Chiral,
Mirror of 160,
Case: 4
πz = (2, 3, 6, 5)(4, 8, 11, 9)(7, 10)
πw = (1, 2, 4, 7, 3)(5, 6, 10, 9, 8)
Reflexible,
Case: 4
πz = (2, 3, 6, 5)(4, 8, 7, 9)(10, 11)
πw = (1, 2, 4, 7, 3)(5, 10, 11, 6, 8)
Reflexible,
Case: 1
πz = (1, 2, 4)(3, 8, 9)(5, 11, 6)(7, 12, 10)
πw = (1, 3, 5)(2, 6, 7)(4, 10, 8)(9, 12, 11)
Reflexible,
Case: 1
πz = (1, 2, 4)(3, 7, 5)(6, 10, 8)(9, 11, 12)
πw = (1, 3)(2, 5, 9, 6)(4, 8, 11, 7)(10, 12)
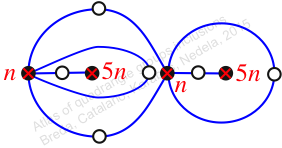
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 9, 8)(10, 11, 12)
πw = (2, 3, 5, 7, 4)(6, 8, 10, 11, 9)
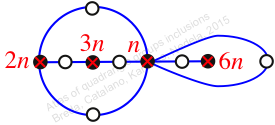
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 12)
πw = (2, 3, 5, 8, 7, 4)(6, 9, 10)(11, 12)
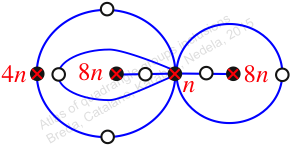
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 8, 9)(10, 12, 11)
πw = (2, 3, 5, 8, 11, 10, 7, 4)(6, 9)
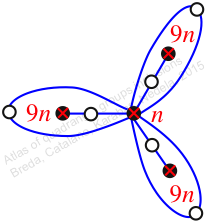
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 12)
πw = (2, 3, 5, 8, 10, 6, 9, 7, 4)
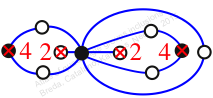
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 9, 8)(10, 11, 12)
πw = (1, 3, 6, 8, 11, 10, 7, 4)(2, 5)(9, 12)
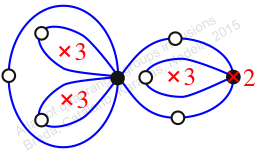
Reflexible,
Case: 2
πz = (2, 3, 5)(4, 6, 7)(8, 10, 9)
πw = (1, 2, 4, 3)(5, 7, 9, 12, 10, 11, 8, 6)
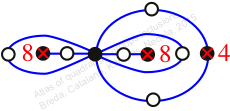
Reflexible,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 8, 9)(10, 12, 11)
πw = (2, 3, 5, 8, 11, 10, 7, 4)(6, 9)
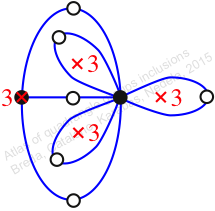
Reflexible,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)
πw = (1, 2, 4, 8, 9, 11, 12, 6, 3)(5, 10, 7)
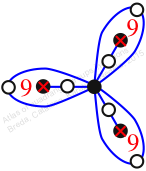
Reflexible,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 12)
πw = (2, 3, 5, 8, 10, 6, 9, 7, 4)
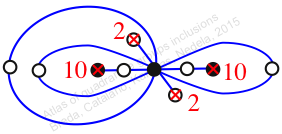
Chiral,
Mirror of 176,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 8, 9)(10, 12, 11)
πw = (2, 3, 5, 7, 9, 11, 10, 8, 6, 4)
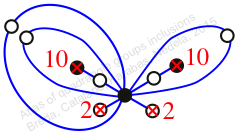
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 8, 10)(9, 11, 12)
πw = (2, 3, 5, 7, 9, 11, 10, 8, 6, 4)
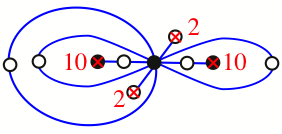
Chiral,
Mirror of 174,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 9, 8)(10, 11, 12)
πw = (2, 3, 5, 6, 8, 10, 11, 9, 7, 4)
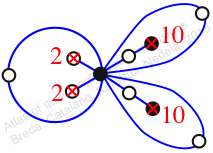
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 12)
πw = (2, 3, 5, 8, 12, 10, 6, 9, 7, 4)
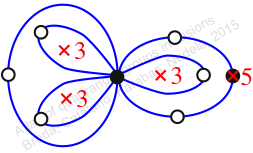
Reflexible,
Case: 2
πz = (2, 3, 5)(6, 8, 7)(9, 10, 11)
πw = (1, 2, 4, 5, 7, 10, 12, 9, 6, 3)(8, 11)
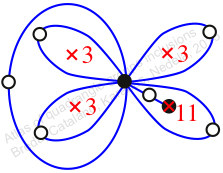
Chiral,
Mirror of 180,
Case: 2
πz = (2, 3, 5)(6, 8, 7)(10, 11, 12)
πw = (1, 2, 4, 5, 7, 10, 11, 8, 9, 6, 3)
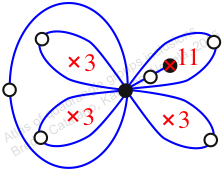
Chiral,
Mirror of 179,
Case: 2
πz = (2, 3, 5)(6, 8, 7)(9, 12, 11)
πw = (1, 2, 4, 5, 7, 10, 8, 11, 9, 6, 3)
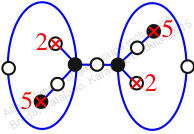
Chiral,
Mirror of 183,
Case: 3
πz = (1, 2, 4, 3)(5, 6, 8, 7)(9, 10, 12, 11)
πw = (2, 3, 5, 6, 4)(7, 9, 11, 10, 8)
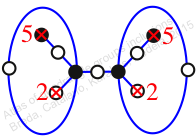
Reflexible,
Case: 3
πz = (1, 2, 4, 3)(5, 6, 8, 7)(9, 10, 11, 12)
πw = (2, 3, 5, 6, 4)(7, 9, 11, 10, 8)
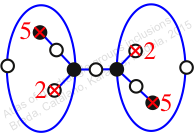
Chiral,
Mirror of 181,
Case: 3
πz = (1, 2, 4, 3)(5, 7, 8, 6)(9, 11, 12, 10)
πw = (2, 3, 4, 6, 5)(7, 8, 10, 11, 9)
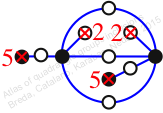
Chiral,
Mirror of 185,
Case: 3
πz = (1, 2, 4, 3)(5, 9, 11, 7)(6, 8, 12, 10)
πw = (2, 3, 6, 9, 5)(4, 7, 11, 10, 8)
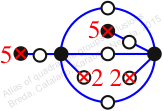
Chiral,
Mirror of 184,
Case: 3
πz = (1, 2, 4, 3)(5, 9, 11, 7)(6, 8, 12, 10)
πw = (2, 3, 6, 10, 5)(4, 7, 9, 12, 8)
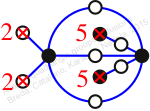
Reflexible,
Case: 3
πz = (1, 2, 4, 3)(5, 9, 10, 7)(6, 8, 12, 11)
πw = (2, 3, 6, 10, 5)(4, 7, 11, 12, 8)
Reflexible,
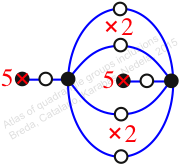
Case: 3
πz = (1, 2, 4, 3)(5, 7)(6, 8)(9, 11, 12, 10)
πw = (2, 3, 6, 9, 5)(4, 7, 10, 11, 8)
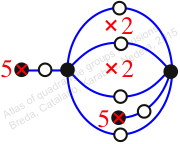
Chiral,
Mirror of 189,
Case: 3
πz = (1, 2, 4, 3)(5, 7)(6, 8, 12, 10)(9, 11)
πw = (2, 3, 6, 9, 5)(4, 7, 11, 10, 8)
Chiral,
Mirror of 188,
Case: 3
πz = (1, 2, 4, 3)(5, 9, 11, 7)(6, 8)(10, 12)
πw = (2, 3, 6, 10, 5)(4, 7, 9, 12, 8)
Reflexible,
Case: 1
πz = (2, 3, 6, 5)(7, 9, 11, 8)
πw = (1, 2, 4, 5, 7, 3)(6, 8, 10, 11, 12, 9)
Reflexible,
Case: 1
πz = (2, 3, 6, 5)(4, 8, 11, 7)
πw = (1, 2, 4, 9, 7, 3)(5, 10, 6, 11, 12, 8)
Reflexible,
Case: 1
πz = (1, 2, 4, 3)(5, 8, 6, 7)(9, 12, 10, 11)
πw = (2, 3, 6, 10, 9, 5)(4, 7)(8, 11)
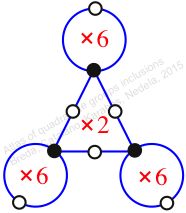
Reflexible,
Case: 1
πz = (1, 2, 4, 3)(5, 9, 10, 7)(6, 8, 11, 12)
πw = (2, 3, 6, 11, 10, 5)(4, 7, 8)
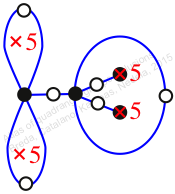
Reflexible,
Case: 3
πz = (2, 3, 4, 7, 5)(8, 9, 12, 10, 11)
πw = (1, 2, 4, 6, 3)(5, 8, 10, 9, 7)
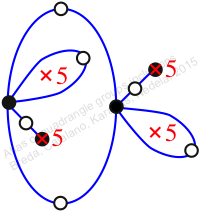
Reflexible,
Case: 3
πz = (2, 3, 6, 4, 5)(7, 9, 10, 11, 8)
πw = (1, 2, 4, 7, 3)(6, 8, 10, 12, 9)
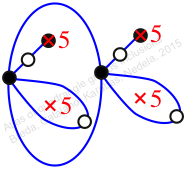
Chiral,
Mirror of 198,
Case: 3
πz = (2, 3, 6, 4, 5)(7, 9, 12, 11, 8)
πw = (1, 2, 4, 7, 3)(6, 8, 10, 11, 9)
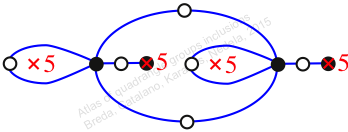
Reflexible,
Case: 3
πz = (2, 3, 6, 10, 5)(4, 8, 11, 7, 9)
πw = (1, 2, 4, 7, 3)(5, 6, 11, 12, 8)
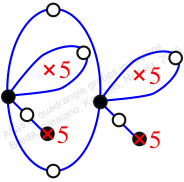
Chiral,
Mirror of 196,
Case: 3
πz = (2, 3, 6, 7, 5)(4, 8, 10, 12, 9)
πw = (1, 2, 4, 7, 3)(5, 9, 10, 11, 8)
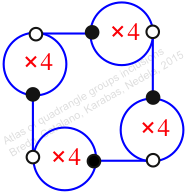
Reflexible,
Case: 1
πz = (1, 7, 2)(3, 5, 10)(4, 9, 11)(6, 8, 12)
πw = (2, 4, 8, 5)(3, 6, 11, 7)
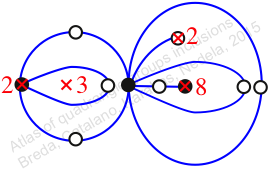
Chiral,
Mirror of 201,
Case: 4
πz = (2, 3, 5)(4, 6, 7)(8, 10, 9)(11, 12, 13)
πw = (1, 2, 4, 3)(5, 7, 9, 11, 12, 10, 8, 6)
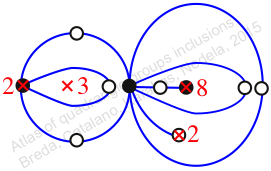
Chiral,
Mirror of 200,
Case: 4
πz = (2, 3, 5)(4, 6, 7)(8, 10, 9)(11, 13, 12)
πw = (1, 2, 4, 3)(5, 7, 9, 10, 12, 11, 8, 6)
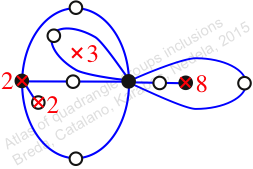
Chiral,
Mirror of 203,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(11, 13, 12)
πw = (1, 2, 4, 8, 12, 11, 6, 3)(5, 10, 9, 7)
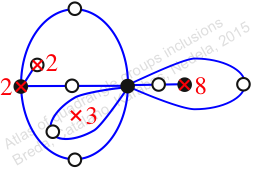
Chiral,
Mirror of 202,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 12, 13)
πw = (1, 2, 4, 8, 12, 9, 6, 3)(5, 10, 11, 7)
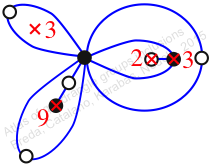
Chiral,
Mirror of 206,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 13, 12)
πw = (1, 2, 4, 7, 5, 9, 11, 6, 3)(10, 12, 13)
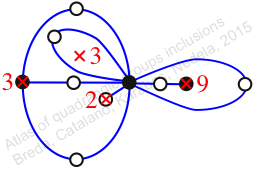
Chiral,
Mirror of 207,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 13, 12)
πw = (1, 2, 4, 8, 10, 12, 11, 6, 3)(5, 9, 7)
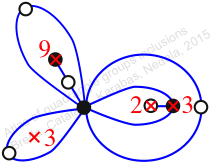
Chiral,
Mirror of 204,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 12, 13)
πw = (1, 2, 4, 8, 7, 5, 10, 6, 3)(9, 13, 12)
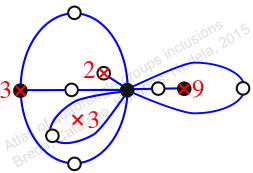
Chiral,
Mirror of 205,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 12, 13)
πw = (1, 2, 4, 8, 12, 9, 11, 6, 3)(5, 10, 7)
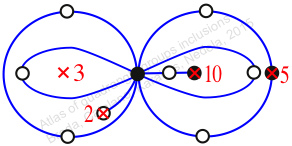
Chiral,
Mirror of 209,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 9, 10)(11, 13, 12)
πw = (1, 2, 4, 6, 9, 12, 11, 8, 5, 3)(7, 10)
Chiral,
Mirror of 208,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 10, 9)(11, 12, 13)
πw = (1, 2, 4, 7, 11, 12, 9, 6, 5, 3)(8, 10)
Chiral,
Mirror of 213,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 12, 13)
πw = (1, 2, 4, 7, 5, 9, 12, 11, 6, 3)(10, 13)
Chiral,
Mirror of 212,
Case: 4
πz = (2, 3, 5)(4, 7, 6)(8, 9, 10)(11, 13, 12)
πw = (1, 2, 4, 8, 10, 12, 11, 9, 6, 3)(5, 7)
Chiral,
Mirror of 211,
Case: 4
πz = (2, 3, 5)(4, 7, 6)(8, 9, 11)(10, 12, 13)
πw = (1, 2, 4, 8, 10, 12, 11, 9, 6, 3)(5, 7)
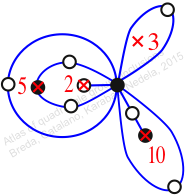
Chiral,
Mirror of 210,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 12)
πw = (1, 2, 4, 8, 12, 7, 5, 10, 6, 3)(9, 13)
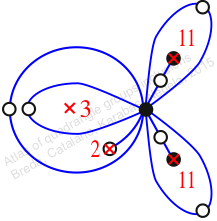
Chiral,
Mirror of 215,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 12, 10)(9, 11, 13)
πw = (1, 2, 4, 6, 9, 11, 7, 10, 8, 5, 3)
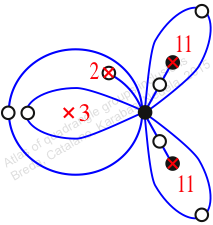
Chiral,
Mirror of 214,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 10, 11)(9, 13, 12)
πw = (1, 2, 4, 7, 10, 8, 12, 9, 6, 5, 3)
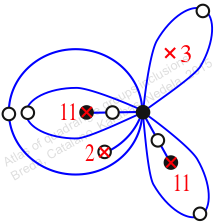
Chiral,
Mirror of 217,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 12, 13)
πw = (1, 2, 4, 7, 5, 9, 11, 12, 10, 6, 3)
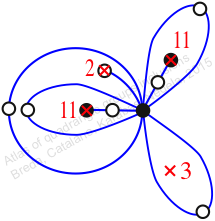
Chiral,
Mirror of 216,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 13, 12)
πw = (1, 2, 4, 7, 5, 9, 10, 12, 11, 6, 3)
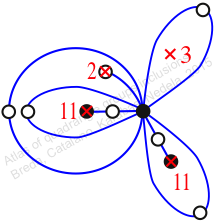
Chiral,
Mirror of 219,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 13, 12)
πw = (1, 2, 4, 8, 12, 11, 7, 5, 9, 6, 3)
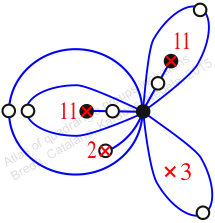
Chiral,
Mirror of 218,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 12, 13)
πw = (1, 2, 4, 8, 12, 9, 7, 5, 10, 6, 3)
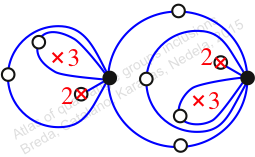
Reflexible,
Case: 3
πz = (2, 3, 4)(5, 7, 6)(8, 10, 9)(11, 12, 13)
πw = (1, 2, 4, 6, 8, 5, 3)(7, 9, 11, 13, 14, 12, 10)
Chiral,
Mirror of 222,
Case: 3
πz = (2, 3, 4)(5, 7, 6)(8, 10, 9)(11, 12, 14)
πw = (1, 2, 4, 6, 8, 5, 3)(7, 9, 11, 13, 14, 12, 10)
Chiral,
Mirror of 221,
Case: 3
πz = (2, 3, 5)(4, 6, 8)(7, 9, 10)(11, 13, 12)
πw = (1, 2, 4, 7, 6, 5, 3)(8, 10, 12, 13, 14, 11, 9)
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 12, 13)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 9, 10, 13, 14, 12, 7)
Chiral,
Mirror of 226,
Case: 3
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 12, 14)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 9, 13, 10, 14, 12, 7)
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(12, 14, 13)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 9, 13, 14, 12, 7)
Chiral,
Mirror of 224,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 14, 13, 9, 12, 7)
Chiral,
Mirror of 228,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 12)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 14, 11, 13, 9, 7)
Chiral,
Mirror of 227,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 11, 14, 9, 13, 7)
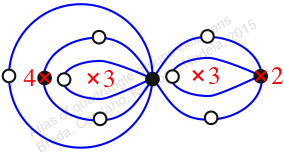
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 6, 7)(8, 10, 9)(11, 12, 13)
πw = (1, 2, 4, 3)(5, 7, 9, 12, 14, 11, 8, 6)(10, 13)
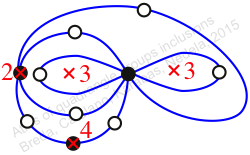
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(12, 13, 14)
πw = (1, 2, 4, 8, 9, 12, 6, 3)(5, 10, 13, 7)(11, 14)
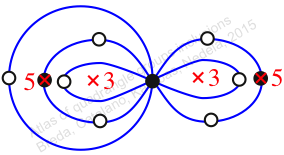
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 6)(8, 9, 11)(10, 13, 12)
πw = (1, 2, 4, 8, 10, 14, 12, 9, 6, 3)(5, 7)(11, 13)
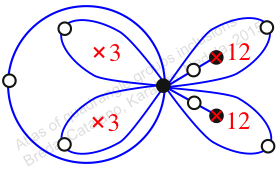
Reflexible,
Case: 3
πz = (2, 3, 5)(6, 8, 7)(9, 13, 11)(10, 12, 14)
πw = (1, 2, 4, 5, 7, 10, 12, 8, 11, 9, 6, 3)
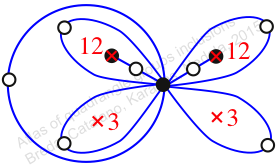
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(12, 13, 14)
πw = (1, 2, 4, 7, 5, 9, 12, 13, 10, 11, 6, 3)
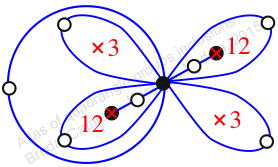
Chiral,
Mirror of 235,
Case: 3
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 14, 13)
πw = (1, 2, 4, 7, 5, 9, 12, 10, 13, 11, 6, 3)
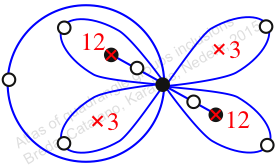
Chiral,
Mirror of 234,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)
πw = (1, 2, 4, 8, 13, 9, 12, 7, 5, 10, 6, 3)
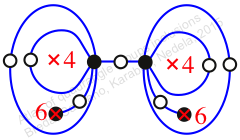
Reflexible,
Case: 3
πz = (2, 3, 4, 5)(6, 8, 9, 7)(10, 12, 14, 11)
πw = (1, 2, 4, 7, 6, 3)(8, 9, 11, 12, 13, 10)
Chiral,
Mirror of 238,
Case: 3
πz = (2, 3, 4, 5)(6, 8, 9, 7)(10, 12, 13, 11)
πw = (1, 2, 4, 7, 6, 3)(8, 9, 11, 14, 13, 10)
Chiral,
Mirror of 237,
Case: 3
πz = (2, 3, 6, 5)(4, 7, 9, 8)(10, 11, 12, 13)
πw = (1, 2, 4, 7, 5, 3)(8, 10, 12, 14, 11, 9)
Chiral,
Mirror of 240,
Case: 3
πz = (2, 3, 6, 5)(4, 8, 9, 10)(7, 13, 14, 12)
πw = (1, 2, 4, 9, 7, 3)(5, 11, 6, 12, 13, 8)
Chiral,
Mirror of 239,
Case: 3
πz = (2, 3, 6, 5)(4, 8, 14, 10)(7, 13, 9, 12)
πw = (1, 2, 4, 9, 7, 3)(5, 11, 6, 12, 10, 8)
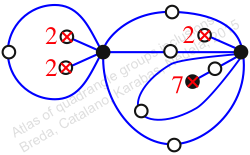
Chiral,
Mirror of 242,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 12)(13, 15, 14)
πw = (2, 3, 5, 8, 11, 7, 4)(6, 9, 12, 14, 15, 13, 10)
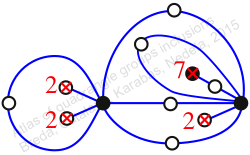
Chiral,
Mirror of 241,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 12)(13, 14, 15)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 13, 15, 14, 11, 10)
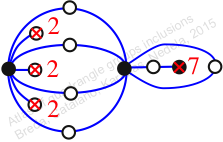
Reflexible,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 15, 14)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 11, 14, 15, 13, 10)
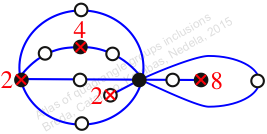
Chiral,
Mirror of 245,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 15, 14)
πw = (2, 3, 5, 8, 12, 11, 7, 4)(6, 9, 14, 10)(13, 15)
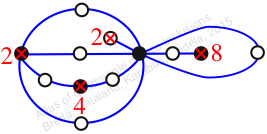
Chiral,
Mirror of 244,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 14, 15)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 14, 10)(11, 15)
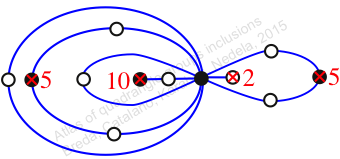
Reflexible,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 8, 9)(10, 12, 11)(13, 14, 15)
πw = (2, 3, 5, 8, 11, 14, 13, 10, 7, 4)(6, 9)(12, 15)
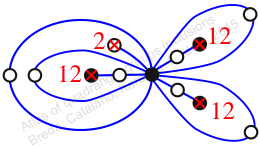
Chiral,
Mirror of 248,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 8, 10)(9, 12, 13)(11, 15, 14)
πw = (2, 3, 5, 7, 9, 12, 10, 14, 11, 8, 6, 4)
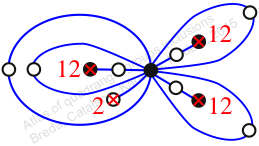
Chiral,
Mirror of 247,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 9, 8)(10, 14, 12)(11, 13, 15)
πw = (2, 3, 5, 6, 8, 11, 13, 9, 12, 10, 7, 4)
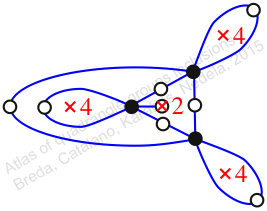
Reflexible,
Case: 2
πz = (2, 3, 6, 5)(4, 8, 10, 7)(9, 11, 14, 12)
πw = (1, 2, 4, 7, 3)(5, 9, 13, 12, 8)(6, 10, 14, 15, 11)
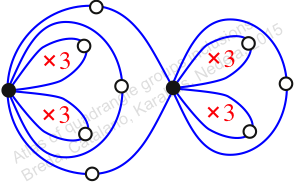
Reflexible,
Case: 1
πz = (2, 3, 5)(6, 8, 7)(9, 11, 10)(12, 13, 15)
πw = (1, 2, 4, 5, 7, 9, 6, 3)(8, 10, 12, 14, 15, 16, 13, 11)
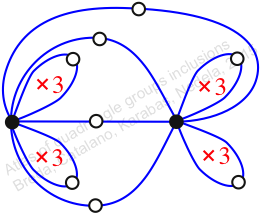
Reflexible,
Case: 1
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(12, 13, 15)
πw = (1, 2, 4, 8, 9, 12, 6, 3)(5, 10, 14, 11, 15, 16, 13, 7)
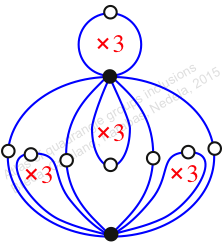
Reflexible,
Case: 1
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 16, 11, 14, 9, 13, 7)
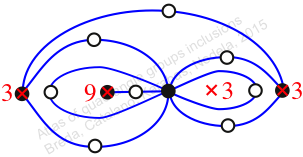
Reflexible,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 12)(14, 15, 16)
πw = (1, 2, 4, 8, 14, 15, 12, 6, 3)(5, 10, 7)(9, 11, 13)
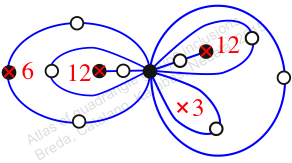
Chiral,
Mirror of 256,
Case: 2
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 12, 13)(14, 16, 15)
πw = (1, 2, 4, 7, 5, 9, 12, 15, 14, 11, 6, 3)(10, 13)
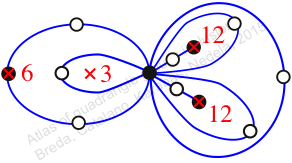
Reflexible,
Case: 2
πz = (2, 3, 5)(4, 7, 6)(8, 9, 11)(10, 13, 14)(12, 16, 15)
πw = (1, 2, 4, 8, 10, 13, 11, 15, 12, 9, 6, 3)(5, 7)
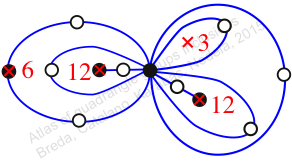
Chiral,
Mirror of 254,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 12)(14, 15, 16)
πw = (1, 2, 4, 8, 14, 15, 12, 7, 5, 10, 6, 3)(9, 13)
Chiral,
Mirror of 258,
Case: 2
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 15, 13)(12, 14, 16)
πw = (1, 2, 4, 7, 5, 9, 12, 14, 10, 13, 11, 6, 3)
Chiral,
Mirror of 257,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)(12, 16, 15)
πw = (1, 2, 4, 8, 13, 9, 15, 12, 7, 5, 10, 6, 3)
Reflexible,
Case: 2
πz = (2, 3)(4, 5, 7, 6)(8, 9, 12, 11)(10, 13, 16, 14)
πw = (1, 2, 4, 5, 3)(6, 8, 10, 9, 7)(11, 15, 12, 14, 13)
Chiral,
Mirror of 261,
Case: 2
πz = (2, 3, 6, 5)(4, 8)(7, 12, 16, 10)(9, 11, 13, 14)
πw = (1, 2, 4, 7, 3)(5, 9, 13, 12, 8)(6, 10, 15, 16, 11)
Chiral,
Mirror of 260,
Case: 2
πz = (2, 3, 6, 5)(4, 8, 13, 9)(7, 11)(10, 12, 16, 15)
πw = (1, 2, 4, 7, 3)(5, 10, 13, 14, 8)(6, 11, 9, 15, 12)
Reflexible,
Case: 1
πz = (1, 2, 4, 3)(5, 9, 13, 7)(6, 8, 11, 12)(10, 14, 16, 15)
πw = (2, 3, 6, 11, 10, 5)(4, 7, 9, 15, 14, 8)
Reflexible,
Case: 1
πz = (1, 2, 4, 3)(5, 9, 13, 7)(6, 8, 14, 12)(10, 16, 11, 15)
πw = (2, 3, 6, 11, 10, 5)(4, 7, 9, 15, 12, 8)
Chiral,
Mirror of 266,
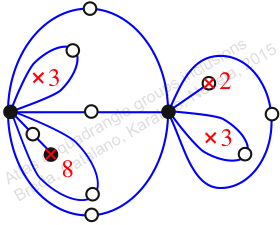
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 12, 10)(9, 11, 13)(15, 17, 16)
πw = (1, 2, 4, 6, 9, 8, 5, 3)(7, 10, 14, 12, 13, 16, 15, 11)
Chiral,
Mirror of 267,
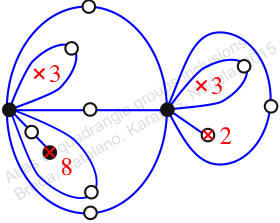
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 12, 10)(9, 11, 13)(14, 16, 17)
πw = (1, 2, 4, 6, 9, 8, 5, 3)(7, 10, 14, 16, 12, 13, 15, 11)
Chiral,
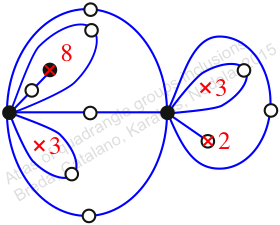
Mirror of 264,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 10, 11)(9, 13, 12)(15, 16, 17)
πw = (1, 2, 4, 7, 9, 6, 5, 3)(8, 12, 15, 16, 13, 11, 14, 10)
Chiral,
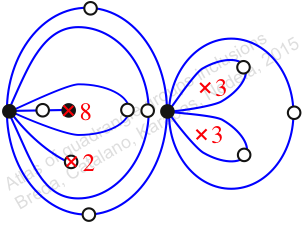
Mirror of 265,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 10, 11)(9, 13, 12)(14, 17, 15)
πw = (1, 2, 4, 7, 9, 6, 5, 3)(8, 12, 16, 13, 11, 15, 14, 10)
Chiral,
Mirror of 269,
Case: 4
πz = (2, 3, 5)(6, 8, 7)(9, 11, 10)(12, 13, 14)(15, 17, 16)
πw = (1, 2, 4, 5, 7, 9, 6, 3)(8, 10, 12, 14, 16, 15, 13, 11)
Chiral,
Mirror of 268,
Case: 4
πz = (2, 3, 5)(6, 8, 7)(9, 11, 10)(12, 13, 15)(14, 16, 17)
πw = (1, 2, 4, 5, 7, 9, 6, 3)(8, 10, 12, 14, 16, 15, 13, 11)
Chiral,
Mirror of 272,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)(15, 17, 16)
πw = (1, 2, 4, 8, 11, 12, 6, 3)(5, 10, 14, 16, 15, 13, 9, 7)
Reflexible,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 12)(15, 16, 17)
πw = (1, 2, 4, 8, 14, 12, 6, 3)(5, 10, 15, 16, 11, 13, 9, 7)
Chiral,
Mirror of 270,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(12, 13, 14)(15, 17, 16)
πw = (1, 2, 4, 8, 9, 12, 6, 3)(5, 10, 11, 14, 16, 15, 13, 7)
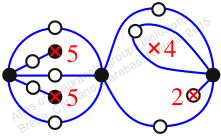
Chiral,
Mirror of 274,
Case: 4
πz = (2, 3, 5, 4)(6, 8, 10, 7)(9, 12, 16, 13)(11, 15, 17, 14)
πw = (1, 2, 4, 6, 3)(5, 7, 9, 11, 8)(10, 14, 15, 13, 12)
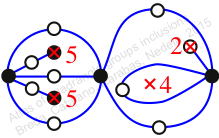
Chiral,
Mirror of 273,
Case: 4
πz = (2, 3, 6, 5)(4, 7, 9, 8)(10, 14, 16, 12)(11, 13, 17, 15)
πw = (1, 2, 4, 6, 3)(5, 8, 11, 10, 7)(9, 12, 14, 15, 13)
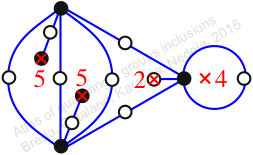
Chiral,
Mirror of 276,
Case: 4
πz = (2, 3, 6, 5)(4, 8, 10, 7)(9, 11, 13, 14)(12, 16, 17, 15)
πw = (1, 2, 4, 7, 3)(5, 9, 13, 12, 8)(6, 10, 15, 16, 11)
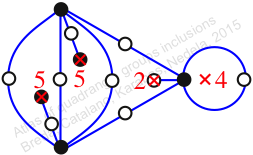
Chiral,
Mirror of 275,
Case: 4
πz = (2, 3, 6, 5)(4, 8, 10, 7)(9, 11, 16, 14)(12, 17, 13, 15)
πw = (1, 2, 4, 7, 3)(5, 9, 13, 12, 8)(6, 10, 15, 14, 11)
Chiral,
Mirror of 278,
Case: 4
πz = (2, 3, 6, 5)(4, 8, 7, 9)(10, 11, 13, 12)(14, 15, 17, 16)
πw = (1, 2, 4, 7, 3)(5, 10, 11, 6, 8)(12, 14, 16, 15, 13)
Chiral,
Mirror of 277,
Case: 4
πz = (2, 3, 6, 5)(4, 8, 7, 9)(10, 11, 13, 12)(14, 15, 16, 17)
πw = (1, 2, 4, 7, 3)(5, 10, 11, 6, 8)(12, 14, 16, 15, 13)
Chiral,
Mirror of 280,
Case: 4
πz = (2, 3, 6, 5)(4, 8, 14, 9)(7, 13, 16, 11)(10, 12, 17, 15)
πw = (1, 2, 4, 7, 3)(5, 10, 13, 9, 8)(6, 11, 16, 15, 12)
Chiral,
Mirror of 279,
Case: 4
πz = (2, 3, 6, 5)(4, 8, 14, 9)(7, 13, 17, 11)(10, 12, 15, 16)
πw = (1, 2, 4, 7, 3)(5, 10, 15, 14, 8)(6, 11, 13, 9, 12)
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 8, 10)(9, 11, 12)(13, 15, 14)(16, 17, 18)
πw = (2, 3, 5, 7, 9, 8, 6, 4)(10, 12, 14, 16, 17, 15, 13, 11)
Chiral,
Mirror of 283,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 8, 10)(9, 11, 12)(13, 15, 14)(16, 18, 17)
πw = (2, 3, 5, 7, 9, 8, 6, 4)(10, 12, 14, 15, 17, 16, 13, 11)
Chiral,
Mirror of 282,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 9, 8)(10, 12, 11)(13, 14, 16)(15, 17, 18)
πw = (2, 3, 5, 6, 8, 10, 7, 4)(9, 11, 13, 15, 17, 16, 14, 12)
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 15, 14)(16, 17, 18)
πw = (2, 3, 5, 8, 12, 11, 7, 4)(6, 9, 14, 16, 17, 15, 13, 10)
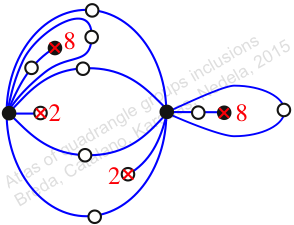
Chiral,
Mirror of 286,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 16, 14)(15, 18, 17)
πw = (2, 3, 5, 8, 12, 11, 7, 4)(6, 9, 14, 16, 13, 17, 15, 10)
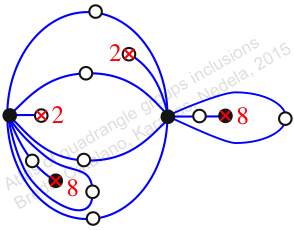
Chiral,
Mirror of 285,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 15, 16)(14, 17, 18)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 14, 17, 11, 16, 15, 10)
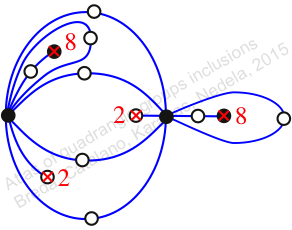
Chiral,
Mirror of 288,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 13, 16)(15, 18, 17)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 11, 16, 14, 17, 15, 10)
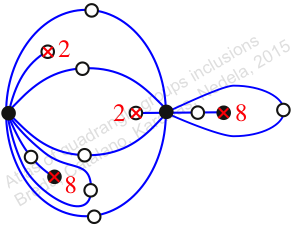
Chiral,
Mirror of 287,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 13, 16)(15, 17, 18)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 17, 11, 16, 14, 10)
Reflexible,
Case: 2
πz = (2, 3, 5)(6, 8, 7)(9, 11, 10)(12, 13, 15)(14, 17, 16)
πw = (1, 2, 4, 5, 7, 9, 6, 3)(8, 10, 12, 14, 18, 16, 13, 11)(15, 17)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 9, 8)(10, 11, 13)(12, 15, 16)(14, 18, 17)
πw = (2, 3, 5, 7, 4)(6, 8, 10, 12, 15, 13, 17, 14, 11, 9)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 8, 9)(10, 12, 11)(13, 14, 15)(16, 18, 17)
πw = (2, 3, 5, 8, 11, 14, 17, 16, 13, 10, 7, 4)(6, 9)(12, 15)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 16, 15)(13, 17, 18)
πw = (2, 3, 5, 8, 13, 17, 14, 11, 15, 12, 7, 4)(6, 9, 10)
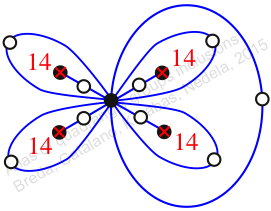
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 15, 16)(14, 18, 17)
πw = (2, 3, 5, 8, 12, 15, 13, 17, 14, 10, 6, 9, 7, 4)
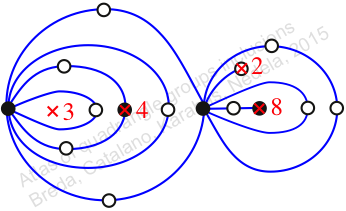
Chiral,
Mirror of 295,
Case: 4
πz = (2, 3, 5)(4, 7, 6)(8, 9, 11)(10, 12, 13)(14, 16, 15)(17, 18, 19)
πw = (1, 2, 4, 8, 10, 9, 6, 3)(5, 7)(11, 13, 15, 17, 18, 16, 14, 12)
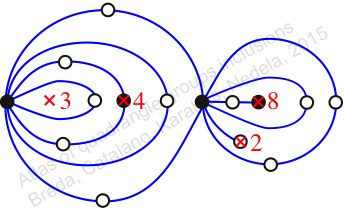
Chiral,
Mirror of 294,
Case: 4
πz = (2, 3, 5)(4, 7, 6)(8, 9, 11)(10, 12, 13)(14, 16, 15)(17, 19, 18)
πw = (1, 2, 4, 8, 10, 9, 6, 3)(5, 7)(11, 13, 15, 16, 18, 17, 14, 12)
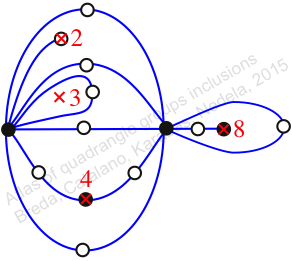
Chiral,
Mirror of 300,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 14, 15)(12, 16, 13)(17, 19, 18)
πw = (1, 2, 4, 8, 13, 11, 6, 3)(5, 9, 14, 16, 18, 17, 12, 7)(10, 15)
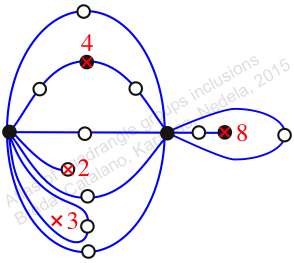
Chiral,
Mirror of 301,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 17, 15)(12, 18, 13)(14, 16, 19)
πw = (1, 2, 4, 8, 13, 11, 6, 3)(5, 9, 14, 16, 10, 15, 12, 7)(17, 18)
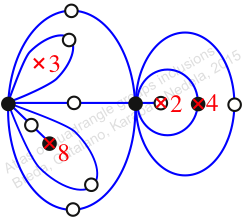
Chiral,
Mirror of 299,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(11, 15, 13)(12, 16, 14)(17, 18, 19)
πw = (1, 2, 4, 8, 13, 11, 6, 3)(5, 10, 9, 14, 18, 17, 12, 7)(16, 19)
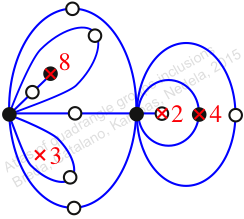
Chiral,
Mirror of 298,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 12, 13)(14, 15, 17)(16, 19, 18)
πw = (1, 2, 4, 8, 12, 9, 6, 3)(5, 10, 14, 16, 18, 15, 11, 7)(17, 19)
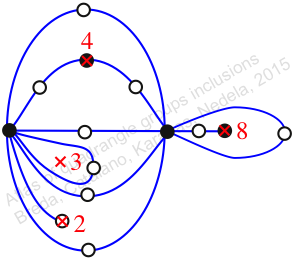
Chiral,
Mirror of 296,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 12)(14, 16, 15)(17, 18, 19)
πw = (1, 2, 4, 8, 14, 11, 6, 3)(5, 10, 15, 17, 18, 16, 12, 7)(9, 13)
Chiral,
Mirror of 297,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 15)(12, 18, 16)(14, 19, 17)
πw = (1, 2, 4, 8, 14, 11, 6, 3)(5, 10, 17, 13, 9, 16, 12, 7)(15, 19)
Chiral,
Mirror of 303,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 13)(12, 15, 17)(16, 18, 19)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 16, 18, 11, 17, 13, 7)(9, 14)
Chiral,
Mirror of 302,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 17, 18)(13, 19, 16)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 17, 14, 9, 16, 13, 7)(11, 18)
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 6)(8, 9, 11)(10, 12, 13)(14, 16, 15)(17, 18, 19)
πw = (1, 2, 4, 8, 10, 9, 6, 3)(5, 7)(11, 13, 15, 18, 20, 17, 14, 12)(16, 19)
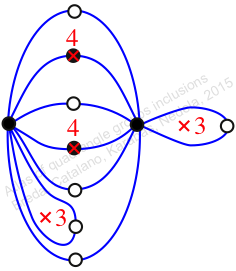
Chiral,
Mirror of 307,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 13)(12, 18, 17)(15, 19, 20)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 16, 11, 17, 19, 13, 7)(9, 14)(18, 20)
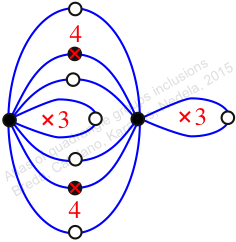
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 13)(12, 16, 17)(15, 18, 19)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 16, 19, 20, 18, 13, 7)(9, 14)(11, 17)
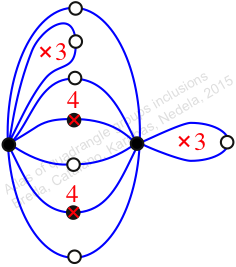
Chiral,
Mirror of 305,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 16)(12, 17, 18)(15, 20, 19)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 17, 19, 14, 9, 13, 7)(11, 18)(16, 20)
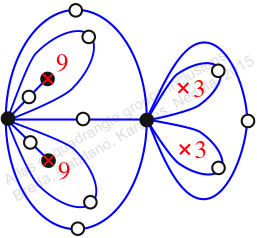
Reflexible,
Case: 3
πz = (2, 3, 5)(6, 8, 7)(9, 13, 11)(10, 12, 14)(15, 17, 19)(16, 20, 18)
πw = (1, 2, 4, 5, 7, 10, 9, 6, 3)(8, 11, 15, 17, 13, 14, 18, 16, 12)
Chiral,
Mirror of 311,
Case: 3
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 13, 12)(14, 15, 17)(18, 20, 19)
πw = (1, 2, 4, 7, 5, 9, 11, 6, 3)(10, 12, 14, 16, 17, 19, 18, 15, 13)
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 13, 12)(14, 15, 17)(16, 19, 20)
πw = (1, 2, 4, 7, 5, 9, 11, 6, 3)(10, 12, 14, 16, 19, 17, 18, 15, 13)
Chiral,
Mirror of 309,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 12, 13)(14, 16, 15)(18, 19, 20)
πw = (1, 2, 4, 8, 7, 5, 10, 6, 3)(9, 13, 15, 18, 19, 16, 17, 14, 12)
Chiral,
Mirror of 314,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 17, 16)(18, 20, 19)
πw = (1, 2, 4, 8, 11, 16, 12, 6, 3)(5, 10, 15, 19, 18, 14, 9, 13, 7)
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 18, 17)(13, 19, 16)
πw = (1, 2, 4, 8, 11, 17, 12, 6, 3)(5, 10, 15, 20, 14, 9, 16, 13, 7)
Chiral,
Mirror of 312,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 13, 17)(18, 20, 19)
πw = (1, 2, 4, 8, 14, 9, 12, 6, 3)(5, 10, 16, 11, 17, 19, 18, 13, 7)
Chiral,
Mirror of 316,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)(15, 18, 19)(16, 17, 20)
πw = (1, 2, 4, 8, 15, 18, 12, 6, 3)(5, 10, 16, 17, 11, 14, 9, 13, 7)
Chiral,
Mirror of 315,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)(13, 19, 16)(15, 18, 20)
πw = (1, 2, 4, 8, 15, 18, 12, 6, 3)(5, 10, 17, 11, 14, 9, 16, 13, 7)
Reflexible,
Case: 1
πz = (2, 3, 6, 5)(4, 8, 13, 9)(7, 12, 15, 11)(14, 17, 19, 16)
πw = (1, 2, 4, 7, 3)(5, 10, 6, 11, 8)(9, 14, 18, 16, 12)(13, 15, 19, 20, 17)
Reflexible,
Case: 1
πz = (2, 3, 6, 5)(4, 8, 14, 9)(7, 13, 18, 11)(10, 12, 17, 16)
πw = (1, 2, 4, 7, 3)(5, 10, 14, 15, 8)(6, 11, 17, 19, 12)(9, 16, 18, 20, 13)
Reflexible,
Case: 1
πz = (2, 3, 6, 5)(4, 8, 14, 9)(7, 13, 18, 11)(10, 12, 19, 16)
πw = (1, 2, 4, 7, 3)(5, 10, 14, 15, 8)(6, 11, 17, 18, 12)(9, 16, 20, 19, 13)
Chiral,
Mirror of 321,
Case: 2
πz = (2, 3, 4)(5, 7, 6)(8, 10, 9)(11, 12, 14)(13, 16, 17)(15, 19, 18)
πw = (1, 2, 4, 6, 8, 5, 3)(7, 9, 11, 13, 15, 12, 10)(14, 18, 21, 19, 17, 20, 16)
Chiral,
Mirror of 320,
Case: 2
πz = (2, 3, 5)(4, 6, 8)(7, 9, 10)(11, 13, 12)(14, 18, 16)(15, 17, 19)
πw = (1, 2, 4, 7, 6, 5, 3)(8, 10, 12, 15, 14, 11, 9)(13, 16, 20, 18, 19, 21, 17)
Chiral,
Mirror of 323,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)(13, 18, 15)(16, 17, 20)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 16, 18, 19, 13, 7)(9, 15, 20, 21, 17, 11, 14)
Chiral,
Mirror of 322,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)(13, 18, 15)(16, 17, 19)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 16, 21, 19, 13, 7)(9, 15, 20, 18, 17, 11, 14)
Chiral,
Mirror of 325,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 8, 10)(9, 12, 13)(11, 15, 14)(16, 20, 17)(18, 19, 21)
πw = (2, 3, 5, 7, 9, 11, 8, 6, 4)(10, 14, 18, 19, 15, 13, 17, 16, 12)
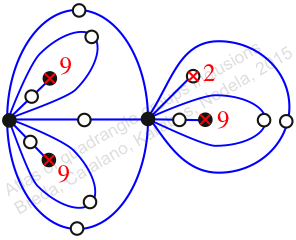
Chiral,
Mirror of 324,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 9, 8)(10, 14, 12)(11, 13, 15)(16, 18, 20)(17, 21, 19)
πw = (2, 3, 5, 6, 8, 11, 10, 7, 4)(9, 12, 16, 18, 14, 15, 19, 17, 13)
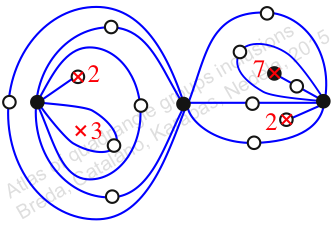
Chiral,
Mirror of 328,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 10, 9)(11, 12, 14)(13, 16, 17)(15, 19, 18)(20, 21, 22)
πw = (1, 2, 4, 6, 8, 5, 3)(7, 9, 11, 13, 15, 12, 10)(14, 18, 20, 21, 19, 17, 16)
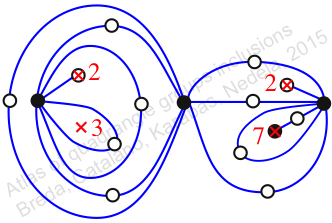
Chiral,
Mirror of 329,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 10, 9)(11, 12, 14)(13, 16, 17)(15, 19, 18)(20, 22, 21)
πw = (1, 2, 4, 6, 8, 5, 3)(7, 9, 11, 13, 15, 12, 10)(14, 18, 19, 17, 21, 20, 16)
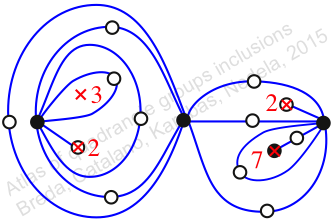
Chiral,
Mirror of 326,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 9, 10)(11, 13, 12)(14, 18, 16)(15, 17, 19)(20, 22, 21)
πw = (1, 2, 4, 7, 6, 5, 3)(8, 10, 12, 15, 14, 11, 9)(13, 16, 18, 19, 21, 20, 17)
Chiral,
Mirror of 327,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 9, 10)(11, 13, 12)(14, 18, 16)(15, 17, 19)(20, 21, 22)
πw = (1, 2, 4, 7, 6, 5, 3)(8, 10, 12, 15, 14, 11, 9)(13, 16, 20, 21, 18, 19, 17)
Chiral,
Mirror of 332,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 12, 14)(13, 15, 17)(16, 19, 18)(20, 21, 22)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 9, 13, 17, 16, 12, 7)(10, 14, 18, 20, 21, 19, 15)
Chiral,
Mirror of 333,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 12, 14)(13, 15, 18)(16, 17, 19)(20, 22, 21)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 9, 13, 17, 16, 12, 7)(10, 14, 19, 18, 21, 20, 15)
Chiral,
Mirror of 330,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)(12, 16, 15)(17, 19, 18)(20, 22, 21)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 14, 18, 16, 12, 7)(9, 15, 19, 21, 20, 17, 13)
Chiral,
Mirror of 331,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)(12, 16, 15)(17, 19, 18)(20, 21, 22)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 14, 19, 17, 12, 7)(9, 15, 20, 21, 16, 18, 13)
Chiral,
Mirror of 335,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)(12, 18, 16)(15, 17, 19)(20, 21, 22)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 15, 19, 13, 9, 7)(11, 16, 20, 21, 18, 14, 17)
Chiral,
Mirror of 334,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 18, 17)(13, 19, 16)(20, 22, 21)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 11, 17, 19, 13, 7)(9, 16, 18, 15, 21, 20, 14)
Chiral,
Mirror of 337,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 18, 17)(13, 19, 16)(20, 21, 22)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 14, 9, 16, 13, 7)(11, 17, 20, 22, 21, 18, 15)
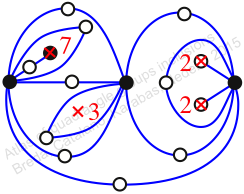
Chiral,
Mirror of 336,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 16, 13)(17, 18, 21)(19, 22, 20)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 18, 11, 13, 7)(9, 16, 15, 20, 22, 19, 14)
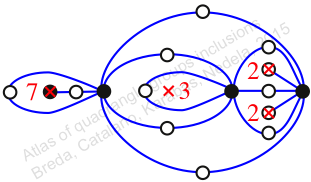
Reflexible,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 18)(13, 17, 16)(20, 22, 21)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 21, 20, 13, 7)(9, 16, 11, 18, 19, 15, 14)

Reflexible,
Case: 3
πz = (2, 3, 6, 5)(4, 8, 7, 9)(10, 11, 13, 12)(14, 15, 18, 17)(16, 19, 22, 20)
πw = (1, 2, 4, 7, 3)(5, 10, 11, 6, 8)(12, 14, 16, 15, 13)(17, 21, 18, 20, 19)
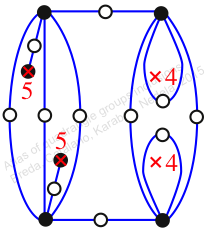
Chiral,
Mirror of 341,
Case: 3
πz = (2, 3, 6, 5)(4, 8, 13, 9)(7, 12, 15, 11)(14, 17, 18, 19)(16, 21, 22, 20)
πw = (1, 2, 4, 7, 3)(5, 10, 6, 11, 8)(9, 14, 18, 16, 12)(13, 15, 20, 21, 17)
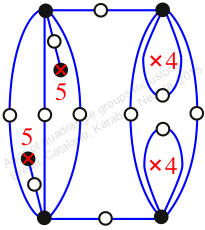
Chiral,
Mirror of 340,
Case: 3
πz = (2, 3, 6, 5)(4, 8, 13, 9)(7, 12, 15, 11)(14, 17, 22, 19)(16, 21, 18, 20)
πw = (1, 2, 4, 7, 3)(5, 10, 6, 11, 8)(9, 14, 18, 16, 12)(13, 15, 20, 19, 17)
Chiral,
Mirror of 343,
Case: 3
πz = (2, 3, 6, 5)(4, 8, 14, 9)(7, 13, 17, 11)(10, 12, 18, 15)(16, 21, 19, 22)
πw = (1, 2, 4, 7, 3)(5, 10, 13, 9, 8)(6, 11, 16, 19, 12)(15, 20, 18, 21, 17)
Chiral,
Mirror of 342,
Case: 3
πz = (2, 3, 6, 5)(4, 8, 14, 9)(7, 13, 18, 11)(10, 12, 19, 17)(15, 21, 16, 20)
πw = (1, 2, 4, 7, 3)(5, 10, 16, 15, 8)(6, 11, 13, 9, 12)(14, 20, 17, 22, 19)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 15)(19, 20, 23)(21, 22, 24)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 19, 20, 15, 10)(11, 16, 21, 22, 18, 13, 17)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 18, 16)(13, 19, 20)(15, 17, 21)(22, 24, 23)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 10)(11, 16, 19, 14, 21, 23, 22, 17)(18, 20)
Reflexible,
Case: 1
πz = (1, 2, 4)(3, 7, 5)(6, 10, 8)(9, 12, 15)(11, 13, 16)(14, 20, 18)(17, 22, 19)(21, 23, 24)
πw = (1, 3)(2, 5, 9, 14, 21, 17, 11, 6)(4, 8, 13, 19, 23, 18, 12, 7)(10, 16)(15, 20)(22, 24)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 14, 15)(16, 18, 17)(19, 23, 21)(20, 22, 24)
πw = (2, 3, 5, 8, 12, 10, 6, 9, 7, 4)(13, 15, 17, 20, 22, 18, 21, 19, 16, 14)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 18, 17)(13, 19, 15)(16, 22, 20)(21, 23, 24)
πw = (2, 3, 5, 8, 13, 11, 17, 12, 7, 4)(6, 9, 15, 21, 23, 19, 14, 20, 16, 10)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 13, 17)(15, 18, 22)(16, 23, 21)(19, 24, 20)
πw = (2, 3, 5, 8, 13, 20, 19, 12, 7, 4)(6, 9, 15, 18, 11, 17, 14, 21, 16, 10)
Reflexible,
Case: 1
πz = (1, 2, 4, 3)(5, 9, 12, 7)(6, 8, 13, 11)(10, 15, 17, 14)(16, 18, 20, 21)(19, 23, 24, 22)
πw = (2, 3, 6, 10, 5)(4, 7, 9, 14, 8)(11, 16, 20, 19, 15)(13, 17, 22, 23, 18)
Chiral,
Mirror of 353,
Case: 1
πz = (1, 2, 4, 3)(5, 9, 12, 7)(6, 8, 13, 11)(10, 15, 17, 14)(16, 18, 23, 21)(19, 24, 20, 22)
πw = (2, 3, 6, 10, 5)(4, 7, 9, 14, 8)(11, 16, 20, 19, 15)(13, 17, 22, 21, 18)
Reflexible,
Case: 1
πz = (1, 2, 4, 3)(5, 9, 10, 7)(6, 8, 12, 11)(13, 15, 17, 14)(16, 19, 23, 20)(18, 22, 24, 21)
πw = (2, 3, 6, 10, 5)(4, 7, 11, 13, 8)(12, 14, 16, 18, 15)(17, 21, 22, 20, 19)
Chiral,
Mirror of 351,
Case: 1
πz = (1, 2, 4, 3)(5, 9, 13, 7)(6, 8, 14, 11)(10, 12, 17, 15)(16, 20, 23, 18)(19, 22, 21, 24)
πw = (2, 3, 6, 10, 5)(4, 7, 12, 11, 8)(9, 15, 19, 21, 16)(13, 18, 20, 22, 17)
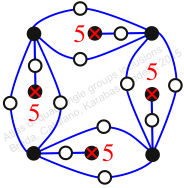
Reflexible,
Case: 1
πz = (1, 2, 4, 3)(5, 9, 13, 7)(6, 8, 14, 11)(10, 18, 23, 16)(12, 19, 15, 20)(17, 22, 24, 21)
πw = (2, 3, 6, 10, 5)(4, 7, 12, 15, 8)(9, 16, 18, 11, 17)(13, 21, 22, 14, 19)
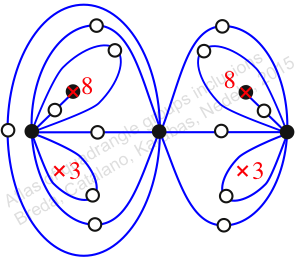
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(11, 15, 13)(12, 16, 14)(17, 21, 19)(18, 20, 22)(24, 26, 25)
πw = (1, 2, 4, 8, 13, 11, 6, 3)(5, 10, 9, 14, 18, 17, 12, 7)(16, 19, 23, 21, 22, 25, 24, 20)
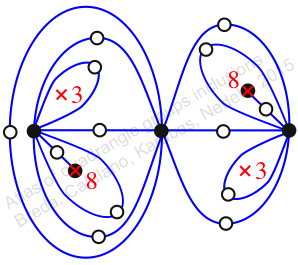
Chiral,
Mirror of 357,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(11, 15, 13)(12, 16, 14)(17, 21, 19)(18, 20, 22)(23, 25, 26)
πw = (1, 2, 4, 8, 13, 11, 6, 3)(5, 10, 9, 14, 18, 17, 12, 7)(16, 19, 23, 25, 21, 22, 24, 20)
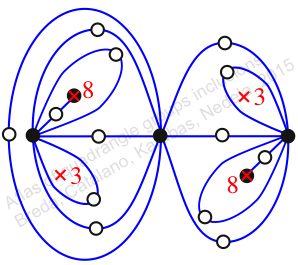
Chiral,
Mirror of 356,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 12, 13)(14, 15, 17)(16, 19, 20)(18, 22, 21)(23, 26, 24)
πw = (1, 2, 4, 8, 12, 9, 6, 3)(5, 10, 14, 16, 18, 15, 11, 7)(17, 21, 25, 22, 20, 24, 23, 19)
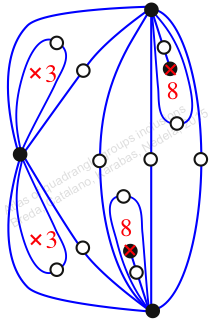
Chiral,
Mirror of 359,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)(13, 19, 16)(17, 18, 21)(20, 24, 23)(22, 26, 25)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 17, 19, 23, 20, 13, 7)(9, 16, 21, 25, 22, 18, 11, 14)
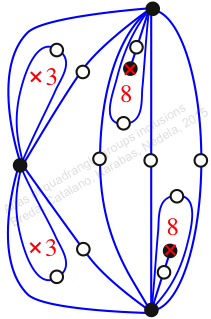
Chiral,
Mirror of 358,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)(13, 19, 16)(17, 18, 20)(21, 23, 25)(22, 24, 26)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 17, 22, 24, 20, 13, 7)(9, 16, 21, 23, 19, 18, 11, 14)
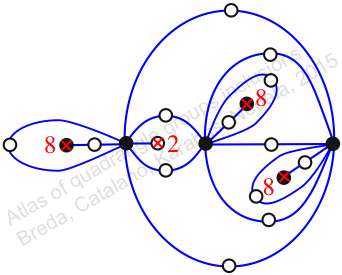
Chiral,
Mirror of 361,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 13, 17)(15, 18, 21)(16, 20, 19)(22, 26, 24)(23, 27, 25)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 20, 24, 22, 16, 10)(11, 17, 14, 19, 21, 25, 23, 18)
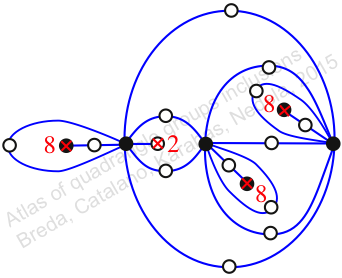
Chiral,
Mirror of 360,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 13, 17)(15, 18, 21)(16, 22, 19)(20, 24, 25)(23, 26, 27)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 20, 24, 21, 16, 10)(11, 17, 14, 19, 23, 26, 22, 18)
Reflexible,
Case: 1
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(12, 14, 13)(15, 17, 16)(18, 19, 21)(20, 23, 24)(22, 26, 25)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 9, 13, 15, 12, 7)(14, 16, 18, 20, 22, 19, 17)(21, 25, 28, 26, 24, 27, 23)
Reflexible,
Case: 1
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 17)(16, 18, 20)(21, 23, 26)(22, 25, 24)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 16, 14, 9, 13, 7)(11, 17, 21, 25, 27, 22, 18)(15, 20, 24, 26, 28, 23, 19)
Chiral,
Mirror of 365,
Case: 1
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 17)(16, 18, 20)(21, 23, 26)(22, 27, 24)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 16, 14, 9, 13, 7)(11, 17, 21, 25, 26, 22, 18)(15, 20, 24, 28, 27, 23, 19)
Chiral,
Mirror of 364,
Case: 1
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 18)(13, 20, 16)(21, 25, 22)(23, 24, 27)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 11, 18, 13, 7)(9, 16, 23, 25, 26, 21, 14)(15, 22, 27, 28, 24, 20, 19)
Reflexible,
Case: 1
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 22)(24, 27, 26)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 25, 22, 13, 7)(9, 16, 24, 20, 15, 23, 14)(11, 18, 26, 28, 27, 21, 19)
Chiral,
Mirror of 368,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 16)(12, 21, 19)(13, 22, 17)(15, 23, 24)(18, 20, 25)(26, 28, 27)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 18, 14, 9, 17, 13, 7)(11, 19, 23, 16, 25, 27, 26, 20)(21, 24)
Chiral,
Mirror of 367,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 16)(12, 21, 19)(13, 22, 17)(15, 24, 23)(18, 20, 26)(25, 27, 28)
πw = (1, 2, 4, 8, 15, 12, 6, 3)(5, 10, 18, 20, 11, 19, 13, 7)(9, 17, 25, 27, 22, 21, 23, 14)(16, 24)
Chiral,
Mirror of 372,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 10, 9)(11, 12, 14)(13, 16, 17)(15, 19, 18)(20, 24, 21)(22, 23, 26)(27, 29, 28)
πw = (1, 2, 4, 6, 8, 5, 3)(7, 9, 11, 13, 15, 12, 10)(14, 18, 22, 24, 25, 20, 16)(17, 21, 26, 28, 27, 23, 19)
Chiral,
Mirror of 371,
Case: 4
πz = (2, 3, 4)(5, 7, 6)(8, 10, 9)(11, 12, 14)(13, 16, 17)(15, 19, 18)(20, 24, 21)(22, 23, 25)(26, 28, 29)
πw = (1, 2, 4, 6, 8, 5, 3)(7, 9, 11, 13, 15, 12, 10)(14, 18, 22, 27, 25, 20, 16)(17, 21, 26, 28, 24, 23, 19)
Chiral,
Mirror of 370,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 9, 10)(11, 13, 12)(14, 18, 16)(15, 17, 19)(20, 22, 25)(21, 24, 23)(27, 29, 28)
πw = (1, 2, 4, 7, 6, 5, 3)(8, 10, 12, 15, 14, 11, 9)(13, 16, 20, 24, 26, 21, 17)(18, 19, 23, 25, 28, 27, 22)
Chiral,
Mirror of 369,
Case: 4
πz = (2, 3, 5)(4, 6, 8)(7, 9, 10)(11, 13, 12)(14, 18, 16)(15, 17, 19)(20, 22, 25)(21, 26, 23)(27, 28, 29)
πw = (1, 2, 4, 7, 6, 5, 3)(8, 10, 12, 15, 14, 11, 9)(13, 16, 20, 24, 25, 21, 17)(18, 19, 23, 27, 28, 26, 22)
Chiral,
Mirror of 376,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 12, 14)(13, 15, 18)(16, 21, 19)(17, 22, 23)(20, 25, 24)(27, 29, 28)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 9, 13, 17, 16, 12, 7)(10, 14, 19, 25, 26, 20, 15)(18, 24, 21, 23, 28, 27, 22)
Chiral,
Mirror of 375,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(12, 14, 13)(15, 17, 16)(18, 19, 21)(20, 23, 24)(22, 26, 25)(27, 28, 29)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 9, 13, 15, 12, 7)(14, 16, 18, 20, 22, 19, 17)(21, 25, 27, 28, 26, 24, 23)
Chiral,
Mirror of 374,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(12, 14, 13)(15, 17, 16)(18, 19, 21)(20, 23, 24)(22, 26, 25)(27, 29, 28)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 9, 13, 15, 12, 7)(14, 16, 18, 20, 22, 19, 17)(21, 25, 26, 24, 28, 27, 23)
Chiral,
Mirror of 373,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)(12, 16, 15)(17, 23, 21)(18, 24, 19)(20, 22, 25)(27, 28, 29)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 14, 19, 17, 12, 7)(9, 15, 20, 26, 25, 18, 13)(16, 21, 27, 28, 23, 24, 22)
Chiral,
Mirror of 380,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)(12, 18, 16)(15, 17, 21)(19, 25, 20)(22, 24, 26)(27, 29, 28)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 15, 19, 13, 9, 7)(11, 16, 22, 25, 21, 23, 17)(14, 20, 26, 28, 27, 24, 18)
Chiral,
Mirror of 379,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)(12, 18, 16)(15, 17, 21)(19, 25, 20)(22, 24, 23)(27, 28, 29)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 15, 19, 13, 9, 7)(11, 16, 22, 27, 28, 23, 17)(14, 20, 26, 25, 21, 24, 18)
Chiral,
Mirror of 378,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 18, 17)(13, 19, 16)(20, 24, 25)(21, 23, 22)(26, 29, 27)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 11, 17, 20, 13, 7)(9, 16, 23, 27, 26, 21, 14)(15, 22, 19, 25, 28, 24, 18)
Chiral,
Mirror of 377,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 18, 17)(13, 19, 16)(20, 24, 25)(21, 26, 22)(27, 28, 29)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 11, 17, 20, 13, 7)(9, 16, 23, 19, 25, 21, 14)(15, 22, 27, 28, 26, 24, 18)
Chiral,
Mirror of 382,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 25)(23, 24, 26)(27, 29, 28)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 24, 21, 13, 7)(9, 16, 23, 20, 15, 22, 14)(11, 18, 26, 25, 28, 27, 19)
Chiral,
Mirror of 381,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 22)(23, 25, 24)(27, 29, 28)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 28, 27, 23, 14)(11, 18, 20, 15, 24, 21, 19)
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 12)(13, 15, 14)(16, 18, 17)(19, 20, 22)(21, 24, 25)(23, 27, 26)(28, 29, 30)
πw = (2, 3, 5, 8, 11, 7, 4)(6, 9, 12, 14, 16, 13, 10)(15, 17, 19, 21, 23, 20, 18)(22, 26, 28, 29, 27, 25, 24)
Chiral,
Mirror of 385,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 12)(13, 15, 14)(16, 18, 17)(19, 20, 22)(21, 24, 25)(23, 27, 26)(28, 30, 29)
πw = (2, 3, 5, 8, 11, 7, 4)(6, 9, 12, 14, 16, 13, 10)(15, 17, 19, 21, 23, 20, 18)(22, 26, 27, 25, 29, 28, 24)
Chiral,
Mirror of 384,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 12)(13, 14, 16)(15, 17, 18)(19, 21, 20)(22, 26, 24)(23, 25, 27)(28, 29, 30)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 13, 15, 14, 11, 10)(16, 18, 20, 23, 22, 19, 17)(21, 24, 28, 29, 26, 27, 25)
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 16, 15)(14, 18, 17)(19, 20, 22)(21, 23, 25)(24, 27, 26)(28, 29, 30)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 11, 15, 19, 14, 10)(13, 17, 21, 25, 24, 20, 16)(18, 22, 26, 28, 29, 27, 23)
Chiral,
Mirror of 388,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 16, 15)(14, 18, 17)(19, 20, 22)(21, 23, 26)(24, 25, 27)(28, 30, 29)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 11, 15, 19, 14, 10)(13, 17, 21, 25, 24, 20, 16)(18, 22, 27, 26, 29, 28, 23)
Chiral,
Mirror of 387,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 17, 15)(14, 16, 19)(18, 22, 20)(21, 25, 23)(24, 27, 26)(28, 29, 30)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 18, 17, 13, 10)(11, 15, 20, 24, 26, 21, 16)(19, 23, 28, 29, 25, 27, 22)
Chiral,
Mirror of 390,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 20)(15, 21, 19)(22, 24, 27)(23, 25, 26)(28, 30, 29)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 22, 15, 10)(11, 16, 23, 21, 27, 24, 17)(13, 19, 26, 29, 28, 25, 18)
Chiral,
Mirror of 389,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 27, 26)(23, 25, 24)(28, 29, 30)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 22, 15, 10)(11, 16, 23, 28, 29, 24, 17)(13, 19, 26, 27, 21, 25, 18)
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 25, 23)(24, 27, 26)(28, 29, 30)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 18, 13, 19, 24, 17)(21, 26, 28, 29, 27, 22, 25)
Chiral,
Mirror of 394,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 27, 23)(24, 25, 26)(28, 30, 29)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 24, 22, 27, 21, 17)(13, 19, 26, 29, 28, 25, 18)
Reflexible,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 27, 28)(23, 24, 25)(26, 29, 30)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 24, 28, 27, 21, 17)(13, 19, 26, 29, 22, 25, 18)
Chiral,
Mirror of 392,
Case: 3
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 27, 23)(24, 26, 25)(28, 29, 30)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 24, 28, 29, 25, 17)(13, 19, 22, 27, 21, 26, 18)
Chiral,
Mirror of 397,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 15, 17)(13, 18, 19)(16, 21, 20)(22, 25, 26)(23, 27, 24)(28, 30, 29)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 19, 24, 22, 16, 10)(11, 17)(14, 20, 25, 27, 29, 28, 23, 18)(21, 26)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 15, 17)(13, 18, 19)(16, 21, 20)(22, 28, 26)(23, 29, 24)(25, 27, 30)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 19, 24, 22, 16, 10)(11, 17)(14, 20, 25, 27, 21, 26, 23, 18)(28, 29)
Chiral,
Mirror of 395,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 19, 17)(13, 20, 16)(15, 18, 22)(21, 26, 24)(23, 25, 28)(27, 29, 30)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 21, 25, 19, 16, 10)(11, 17, 23, 27, 29, 28, 24, 18)(14, 20)(22, 26)
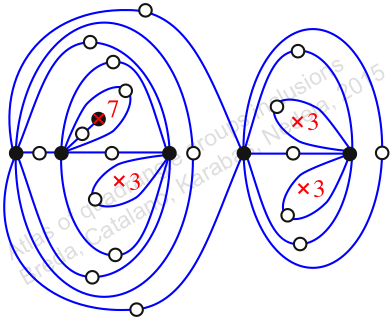
Chiral,
Mirror of 399,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(12, 14, 13)(15, 17, 16)(18, 19, 21)(20, 23, 24)(22, 26, 25)(27, 31, 28)(29, 30, 33)(34, 36, 35)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 9, 13, 15, 12, 7)(14, 16, 18, 20, 22, 19, 17)(21, 25, 29, 31, 32, 27, 23)(24, 28, 33, 35, 34, 30, 26)
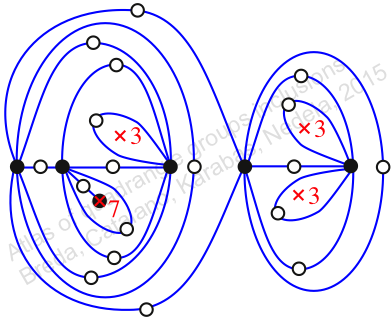
Chiral,
Mirror of 398,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 8, 10)(12, 14, 13)(15, 17, 16)(18, 19, 21)(20, 23, 24)(22, 26, 25)(27, 31, 28)(29, 30, 32)(33, 35, 36)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 9, 13, 15, 12, 7)(14, 16, 18, 20, 22, 19, 17)(21, 25, 29, 34, 32, 27, 23)(24, 28, 33, 35, 31, 30, 26)
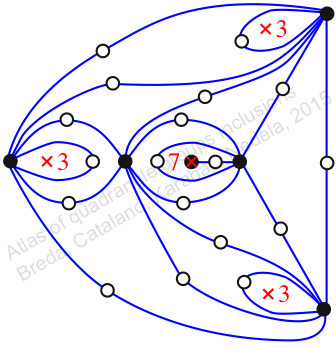
Chiral,
Mirror of 401,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 26)(22, 31, 29)(24, 30, 27)(25, 32, 33)(34, 35, 36)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 25, 22, 13, 7)(9, 16, 24, 20, 15, 23, 14)(11, 18, 27, 32, 26, 28, 19)(21, 29, 34, 35, 31, 33, 30)
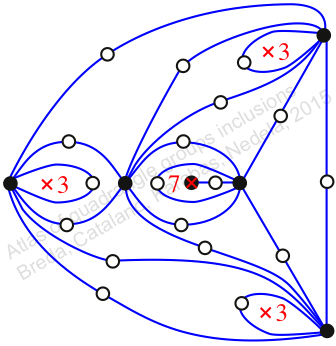
Chiral,
Mirror of 400,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 22)(23, 30, 24)(25, 29, 31)(27, 28, 32)(34, 36, 35)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 33, 31, 23, 14)(11, 18, 27, 30, 29, 21, 19)(15, 24, 32, 35, 34, 28, 20)
Chiral,
Mirror of 404,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 19, 17)(13, 20, 21)(15, 18, 23)(16, 24, 22)(25, 29, 26)(27, 28, 31)(30, 34, 33)(32, 36, 35)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 18, 11, 17, 16, 10)(14, 22, 27, 29, 33, 30, 25, 20)(19, 21, 26, 31, 35, 32, 28, 24)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 19, 17)(13, 20, 21)(15, 18, 23)(16, 24, 22)(25, 29, 26)(27, 28, 30)(31, 33, 35)(32, 34, 36)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 18, 11, 17, 16, 10)(14, 22, 27, 32, 34, 30, 25, 20)(19, 21, 26, 31, 33, 29, 28, 24)
Chiral,
Mirror of 402,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 19, 17)(13, 20, 21)(15, 18, 23)(16, 24, 22)(25, 27, 30)(26, 31, 28)(29, 33, 34)(32, 35, 36)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 20, 14, 22, 16, 10)(11, 17, 25, 29, 33, 30, 26, 18)(19, 21, 23, 28, 32, 35, 31, 27)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 14)(12, 19, 17)(13, 20, 21)(15, 18, 24)(16, 23, 22)(25, 32, 30)(26, 28, 33)(27, 29, 31)(34, 36, 35)
πw = (2, 3, 5, 8, 13, 12, 7, 4)(6, 9, 15, 23, 30, 25, 16, 10)(11, 17, 26, 28, 19, 21, 27, 18)(14, 22, 24, 31, 35, 34, 29, 20)
Chiral,
Mirror of 407,
Case: 4
πz = (2, 3, 5)(4, 7, 8)(6, 10, 9)(11, 12, 14)(13, 15, 18)(16, 21, 19)(17, 22, 23)(20, 26, 24)(25, 28, 32)(27, 30, 29)(31, 33, 35)(34, 37, 36)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 9, 13, 17, 16, 12, 7)(10, 14, 19, 25, 27, 20, 15)(18, 24, 31, 33, 26, 29, 22)(21, 23, 30, 32, 36, 34, 28)
Chiral,
Mirror of 406,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 13, 14)(12, 16, 15)(17, 23, 21)(18, 24, 19)(20, 22, 27)(25, 32, 31)(26, 28, 30)(29, 34, 33)(35, 36, 37)
πw = (1, 2, 4, 8, 11, 6, 3)(5, 10, 14, 19, 17, 12, 7)(9, 15, 20, 26, 25, 18, 13)(16, 21, 28, 27, 33, 29, 22)(23, 24, 31, 35, 36, 32, 30)
Chiral,
Mirror of 409,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)(13, 18, 15)(16, 17, 22)(19, 26, 24)(20, 25, 27)(21, 28, 29)(23, 31, 30)(32, 36, 33)(34, 37, 35)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 16, 21, 19, 13, 7)(9, 15, 20, 23, 17, 11, 14)(18, 24, 31, 27, 33, 32, 25)(22, 30, 26, 29, 35, 34, 28)
Chiral,
Mirror of 408,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 12)(13, 18, 15)(16, 17, 22)(19, 26, 24)(20, 25, 27)(21, 28, 29)(23, 31, 30)(32, 33, 36)(34, 35, 37)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 16, 21, 19, 13, 7)(9, 15, 20, 23, 17, 11, 14)(18, 24, 32, 33, 26, 29, 25)(22, 30, 34, 35, 31, 27, 28)
Chiral,
Mirror of 412,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 18, 17)(13, 19, 16)(20, 21, 23)(22, 24, 25)(26, 28, 27)(29, 33, 31)(30, 32, 34)(35, 37, 36)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 14, 9, 16, 13, 7)(11, 17, 20, 22, 21, 18, 15)(23, 25, 27, 30, 29, 26, 24)(28, 31, 33, 34, 36, 35, 32)
Chiral,
Mirror of 413,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 18, 17)(13, 19, 16)(20, 21, 23)(22, 24, 25)(26, 28, 27)(29, 33, 31)(30, 32, 34)(35, 36, 37)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 14, 9, 16, 13, 7)(11, 17, 20, 22, 21, 18, 15)(23, 25, 27, 30, 29, 26, 24)(28, 31, 35, 36, 33, 34, 32)
Chiral,
Mirror of 410,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 16, 13)(17, 18, 21)(19, 22, 20)(23, 25, 24)(26, 27, 29)(28, 31, 32)(30, 34, 33)(35, 36, 37)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 18, 11, 13, 7)(9, 16, 15, 20, 23, 19, 14)(22, 24, 26, 28, 30, 27, 25)(29, 33, 35, 36, 34, 32, 31)
Chiral,
Mirror of 411,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 16, 13)(17, 18, 21)(19, 22, 20)(23, 25, 24)(26, 27, 29)(28, 31, 32)(30, 34, 33)(35, 37, 36)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 18, 11, 13, 7)(9, 16, 15, 20, 23, 19, 14)(22, 24, 26, 28, 30, 27, 25)(29, 33, 34, 32, 36, 35, 31)
Chiral,
Mirror of 415,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 18)(13, 17, 16)(20, 26, 23)(21, 27, 22)(24, 25, 29)(28, 31, 32)(30, 34, 33)(35, 36, 37)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 23, 20, 13, 7)(9, 16, 11, 18, 24, 21, 14)(15, 22, 28, 32, 30, 25, 19)(27, 29, 33, 35, 36, 34, 31)
Chiral,
Mirror of 414,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 18)(13, 17, 16)(20, 26, 23)(21, 27, 22)(24, 25, 29)(28, 31, 33)(30, 32, 34)(35, 37, 36)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 23, 20, 13, 7)(9, 16, 11, 18, 24, 21, 14)(15, 22, 28, 32, 30, 25, 19)(27, 29, 34, 33, 36, 35, 31)
Chiral,
Mirror of 417,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 23)(22, 30, 28)(24, 29, 32)(25, 31, 33)(26, 27, 34)(35, 36, 37)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 25, 22, 13, 7)(9, 16, 24, 32, 31, 23, 14)(11, 18, 26, 27, 20, 15, 19)(21, 28, 35, 36, 30, 33, 29)
Chiral,
Mirror of 416,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 26)(22, 29, 28)(23, 30, 24)(25, 31, 32)(27, 34, 33)(35, 37, 36)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 25, 22, 13, 7)(9, 16, 20, 15, 24, 23, 14)(11, 18, 21, 28, 34, 27, 19)(26, 33, 29, 32, 36, 35, 31)
Chiral,
Mirror of 420,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 27)(22, 24, 23)(25, 31, 33)(26, 34, 32)(28, 30, 29)(35, 36, 37)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 31, 21, 23, 14)(11, 18, 28, 35, 36, 29, 19)(15, 24, 32, 34, 27, 30, 20)
Reflexible,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 27)(22, 26, 31)(23, 25, 24)(28, 30, 29)(32, 36, 33)(34, 35, 37)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 33, 32, 23, 14)(11, 18, 28, 34, 35, 29, 19)(15, 24, 21, 31, 27, 30, 20)
Chiral,
Mirror of 418,
Case: 4
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 27)(22, 32, 31)(23, 25, 24)(26, 28, 30)(29, 36, 35)(33, 37, 34)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 34, 33, 23, 14)(11, 18, 28, 27, 35, 29, 19)(15, 24, 21, 31, 32, 30, 20)
Chiral,
Mirror of 427,
Case: 3
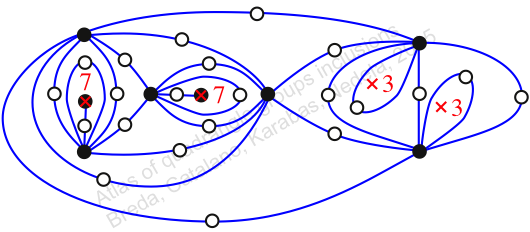
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 17)(16, 18, 20)(21, 23, 26)(22, 27, 24)(25, 31, 32)(28, 36, 34)(29, 37, 33)(30, 35, 38)(39, 42, 43)(40, 41, 44)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 16, 14, 9, 13, 7)(11, 17, 21, 25, 28, 22, 18)(15, 20, 24, 30, 29, 23, 19)(26, 33, 39, 42, 37, 38, 31)(27, 34, 40, 41, 36, 32, 35)
Chiral,
Mirror of 428,
Case: 3
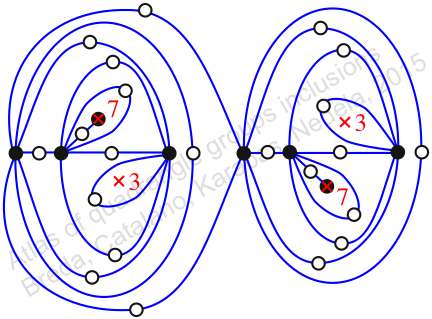
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 17)(16, 18, 20)(21, 23, 26)(22, 27, 24)(25, 31, 32)(28, 36, 34)(29, 37, 33)(30, 35, 38)(39, 43, 40)(41, 44, 42)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 16, 14, 9, 13, 7)(11, 17, 21, 25, 28, 22, 18)(15, 20, 24, 30, 29, 23, 19)(26, 33, 36, 32, 40, 39, 31)(27, 34, 37, 38, 42, 41, 35)
Reflexible,
Case: 3
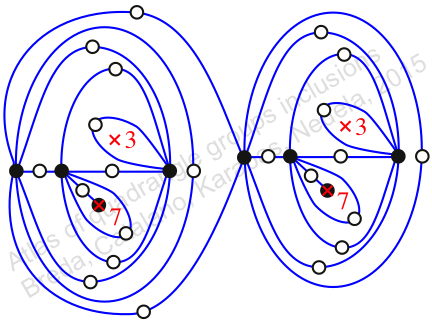
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 18, 17)(13, 19, 16)(20, 21, 23)(22, 24, 25)(26, 28, 27)(29, 33, 31)(30, 32, 34)(35, 37, 40)(36, 39, 38)(42, 44, 43)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 14, 9, 16, 13, 7)(11, 17, 20, 22, 21, 18, 15)(23, 25, 27, 30, 29, 26, 24)(28, 31, 35, 39, 41, 36, 32)(33, 34, 38, 40, 43, 42, 37)
Chiral,
Mirror of 425,
Case: 3
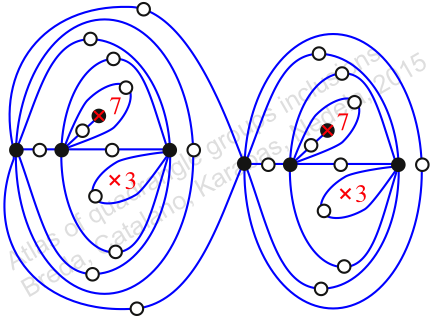
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 18, 17)(13, 19, 16)(20, 21, 23)(22, 24, 25)(26, 28, 27)(29, 33, 31)(30, 32, 34)(35, 37, 40)(36, 41, 38)(42, 43, 44)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 14, 9, 16, 13, 7)(11, 17, 20, 22, 21, 18, 15)(23, 25, 27, 30, 29, 26, 24)(28, 31, 35, 39, 40, 36, 32)(33, 34, 38, 42, 43, 41, 37)
Chiral,
Mirror of 424,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 16, 13)(17, 18, 21)(19, 22, 20)(23, 25, 24)(26, 27, 29)(28, 31, 32)(30, 34, 33)(35, 39, 36)(37, 38, 41)(42, 44, 43)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 18, 11, 13, 7)(9, 16, 15, 20, 23, 19, 14)(22, 24, 26, 28, 30, 27, 25)(29, 33, 37, 39, 40, 35, 31)(32, 36, 41, 43, 42, 38, 34)
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 18)(13, 17, 16)(20, 26, 23)(21, 27, 22)(24, 25, 29)(28, 31, 33)(30, 35, 34)(32, 37, 38)(36, 40, 39)(42, 44, 43)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 23, 20, 13, 7)(9, 16, 11, 18, 24, 21, 14)(15, 22, 28, 32, 30, 25, 19)(27, 29, 34, 40, 41, 36, 31)(33, 39, 35, 38, 43, 42, 37)
Chiral,
Mirror of 421,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 18)(13, 20, 16)(21, 25, 22)(23, 24, 29)(26, 33, 31)(27, 32, 34)(28, 35, 36)(30, 38, 37)(39, 43, 40)(41, 44, 42)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 11, 18, 13, 7)(9, 16, 23, 28, 26, 21, 14)(15, 22, 27, 30, 24, 20, 19)(25, 31, 38, 34, 40, 39, 32)(29, 37, 33, 36, 42, 41, 35)
Chiral,
Mirror of 422,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 18)(13, 20, 16)(21, 25, 22)(23, 24, 29)(26, 33, 31)(27, 32, 34)(28, 35, 36)(30, 38, 37)(39, 40, 43)(41, 42, 44)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 11, 18, 13, 7)(9, 16, 23, 28, 26, 21, 14)(15, 22, 27, 30, 24, 20, 19)(25, 31, 39, 40, 33, 36, 32)(29, 37, 41, 42, 38, 34, 35)
Chiral,
Mirror of 431,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 23)(22, 30, 28)(24, 29, 33)(25, 31, 34)(26, 27, 35)(32, 39, 40)(36, 38, 41)(42, 44, 43)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 25, 22, 13, 7)(9, 16, 24, 32, 31, 23, 14)(11, 18, 26, 27, 20, 15, 19)(21, 28, 36, 39, 33, 37, 29)(30, 34, 40, 41, 43, 42, 38)
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 23)(22, 30, 28)(24, 29, 33)(25, 31, 34)(26, 27, 35)(32, 39, 40)(36, 38, 37)(41, 42, 44)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 25, 22, 13, 7)(9, 16, 24, 32, 31, 23, 14)(11, 18, 26, 27, 20, 15, 19)(21, 28, 36, 41, 42, 37, 29)(30, 34, 40, 43, 39, 33, 38)
Chiral,
Mirror of 429,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 26)(22, 29, 28)(23, 30, 24)(25, 31, 32)(27, 34, 33)(35, 36, 40)(37, 41, 38)(42, 43, 44)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 25, 22, 13, 7)(9, 16, 20, 15, 24, 23, 14)(11, 18, 21, 28, 35, 27, 19)(26, 33, 39, 34, 40, 37, 31)(29, 32, 38, 42, 43, 41, 36)
Chiral,
Mirror of 435,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 27)(22, 24, 23)(25, 31, 33)(26, 34, 32)(28, 30, 37)(29, 38, 35)(39, 40, 41)(42, 44, 43)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 31, 21, 23, 14)(11, 18, 28, 36, 37, 29, 19)(15, 24, 32, 39, 38, 30, 20)(27, 35, 41, 43, 42, 40, 34)
Reflexible,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 27)(22, 32, 31)(23, 25, 24)(26, 35, 36)(28, 30, 37)(33, 40, 34)(38, 39, 41)(42, 44, 43)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 34, 33, 23, 14)(11, 18, 28, 35, 27, 29, 19)(15, 24, 21, 31, 38, 30, 20)(32, 36, 37, 41, 43, 42, 39)
Chiral,
Mirror of 436,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 27)(22, 32, 31)(23, 25, 24)(26, 35, 36)(28, 30, 39)(29, 40, 37)(33, 41, 34)(42, 44, 43)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 34, 33, 23, 14)(11, 18, 28, 38, 39, 29, 19)(15, 24, 21, 31, 40, 30, 20)(27, 37, 32, 36, 43, 42, 35)
Chiral,
Mirror of 432,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 27)(22, 33, 31)(23, 34, 24)(25, 32, 36)(26, 28, 30)(29, 38, 37)(39, 41, 40)(42, 43, 44)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 34, 35, 23, 14)(11, 18, 28, 27, 37, 29, 19)(15, 24, 36, 41, 33, 30, 20)(21, 31, 39, 42, 43, 40, 32)
Chiral,
Mirror of 434,
Case: 3
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 20, 18)(13, 21, 16)(17, 19, 27)(22, 33, 31)(23, 34, 24)(25, 32, 36)(26, 37, 38)(28, 30, 29)(39, 40, 43)(41, 42, 44)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 26, 22, 13, 7)(9, 16, 25, 34, 35, 23, 14)(11, 18, 28, 39, 40, 29, 19)(15, 24, 36, 37, 27, 30, 20)(21, 31, 41, 42, 33, 38, 32)
Chiral,
Mirror of 438,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 16, 15)(14, 18, 17)(19, 20, 22)(21, 23, 26)(24, 29, 27)(25, 30, 31)(28, 34, 32)(33, 36, 40)(35, 38, 37)(39, 41, 43)(42, 45, 44)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 11, 15, 19, 14, 10)(13, 17, 21, 25, 24, 20, 16)(18, 22, 27, 33, 35, 28, 23)(26, 32, 39, 41, 34, 37, 30)(29, 31, 38, 40, 44, 42, 36)
Chiral,
Mirror of 437,
Case: 2
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 17, 15)(14, 16, 19)(18, 22, 20)(21, 25, 23)(24, 27, 29)(26, 32, 30)(28, 31, 35)(33, 40, 36)(34, 37, 39)(38, 43, 41)(42, 44, 45)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 18, 17, 13, 10)(11, 15, 20, 24, 26, 21, 16)(19, 23, 28, 34, 33, 27, 22)(25, 30, 37, 35, 41, 38, 31)(29, 36, 42, 44, 40, 39, 32)
Reflexible,
Case: 2
πz = (2, 3, 5)(4, 7, 9)(6, 11, 10)(8, 14, 15)(12, 19, 18)(13, 17, 16)(20, 26, 23)(21, 27, 22)(24, 25, 29)(28, 31, 33)(30, 35, 34)(32, 37, 38)(36, 42, 39)(40, 41, 47)(43, 45, 44)(46, 49, 50)(48, 52, 51)
πw = (1, 2, 4, 8, 12, 6, 3)(5, 10, 17, 23, 20, 13, 7)(9, 16, 11, 18, 24, 21, 14)(15, 22, 28, 32, 30, 25, 19)(27, 29, 34, 40, 43, 36, 31)(33, 39, 46, 49, 42, 44, 37)(35, 38, 45, 47, 51, 48, 41)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 24, 26)(23, 31, 29)(25, 32, 28)(27, 30, 34)(33, 37, 35)(36, 40, 38)(39, 42, 44)(41, 47, 45)(43, 46, 50)(48, 55, 51)(49, 52, 54)(53, 58, 56)(57, 59, 60)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 24, 21, 28, 25, 17)(13, 19, 27, 33, 31, 26, 18)(22, 29, 35, 39, 41, 36, 30)(34, 38, 43, 49, 48, 42, 37)(40, 45, 52, 50, 56, 53, 46)(44, 51, 57, 59, 55, 54, 47)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 28, 29)(23, 32, 30)(24, 26, 25)(27, 31, 35)(33, 34, 39)(36, 38, 42)(37, 43, 40)(41, 47, 48)(44, 52, 50)(45, 53, 49)(46, 51, 54)(55, 58, 59)(56, 57, 60)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 24, 33, 34, 25, 17)(13, 19, 27, 28, 21, 26, 18)(22, 30, 36, 41, 44, 37, 31)(29, 35, 40, 46, 45, 38, 32)(42, 49, 55, 58, 53, 54, 47)(43, 50, 56, 57, 52, 48, 51)
Chiral,
Mirror of 443,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 28, 29)(23, 32, 30)(24, 26, 25)(27, 31, 35)(33, 34, 39)(36, 38, 42)(37, 43, 40)(41, 47, 48)(44, 52, 50)(45, 53, 49)(46, 51, 54)(55, 59, 56)(57, 60, 58)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 24, 33, 34, 25, 17)(13, 19, 27, 28, 21, 26, 18)(22, 30, 36, 41, 44, 37, 31)(29, 35, 40, 46, 45, 38, 32)(42, 49, 52, 48, 56, 55, 47)(43, 50, 53, 54, 58, 57, 51)
Chiral,
Mirror of 442,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 28, 29)(23, 32, 31)(24, 26, 27)(25, 33, 30)(34, 40, 35)(36, 41, 37)(38, 39, 45)(42, 49, 47)(43, 48, 50)(44, 51, 52)(46, 54, 53)(55, 56, 59)(57, 58, 60)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 24, 22, 31, 25, 17)(13, 19, 27, 35, 34, 26, 18)(21, 30, 38, 44, 42, 36, 28)(29, 37, 43, 46, 39, 33, 32)(41, 47, 55, 56, 49, 52, 48)(45, 53, 57, 58, 54, 50, 51)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 28, 29)(23, 33, 31)(24, 26, 35)(25, 36, 30)(27, 32, 40)(34, 47, 48)(37, 42, 41)(38, 51, 49)(39, 44, 46)(43, 50, 53)(45, 54, 52)(55, 57, 56)(58, 60, 59)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 24, 34, 37, 25, 17)(13, 19, 27, 39, 38, 26, 18)(21, 30, 43, 50, 36, 41, 28)(22, 31, 44, 40, 52, 45, 32)(29, 42, 48, 56, 51, 46, 33)(35, 49, 57, 59, 58, 55, 47)
Reflexible,
Case: 1
πz = (1, 2, 3)(4, 6, 5)(7, 11, 9)(8, 10, 13)(12, 18, 16)(14, 17, 21)(15, 22, 19)(20, 28, 29)(23, 33, 31)(24, 26, 35)(25, 36, 30)(27, 32, 40)(34, 47, 48)(37, 42, 41)(38, 51, 49)(39, 52, 53)(43, 50, 54)(44, 46, 45)(55, 56, 59)(57, 58, 60)
πw = (2, 3, 5, 8, 12, 7, 4)(6, 9, 14, 20, 23, 15, 10)(11, 16, 24, 34, 37, 25, 17)(13, 19, 27, 39, 38, 26, 18)(21, 30, 43, 50, 36, 41, 28)(22, 31, 44, 55, 56, 45, 32)(29, 42, 48, 52, 40, 46, 33)(35, 49, 57, 58, 51, 53, 47)